Advertisements
Advertisements
Question
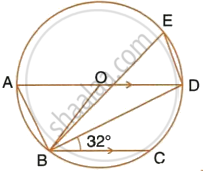
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
Find:
- ∠OBD
- ∠AOB
- ∠BED
Solution
i. AD is parallel to BC, i.e., OD is parallel to BC and BD is transversal
`=>` ∠ODB = ∠CBD = 32° ...(Alternate angles)
In ΔOBD,
OD = OB ...(Radii of the same circle)
`=>` ∠ODB = ∠OBD = 32°
ii. AD is parallel to BC, i.e., AO is parallel to BC and OB is transversal.
`=>` ∠AOB = ∠OBC ...(Alternate angles)
`=>` ∠OBC = ∠OBD + ∠DBC
`=>` ∠OBC = 32° + 32°
`=>` ∠OBC = 64°
`=>` ∠AOB = 64°
iii. In ΔOAB,
OA = OB ...(Radii of the same circle)
`=>` ∠OAB = ∠OBA = x ...(say)
`=>` ∠OAB + ∠OBA + ∠AOB = 180°
`=>` x + x + 64° = 180°
`=>` 2x = 180° – 64°
`=>` 2x = 116°
`=>` x = 58°
`=>` ∠OAB = 58°
i.e. ∠DAB = 58°
`=>` ∠DAB = ∠BED = 58° ...(Angles inscribed in the same arc are equal)
APPEARS IN
RELATED QUESTIONS
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
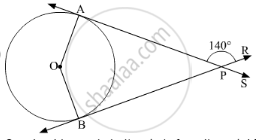
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 140°.
PQ is a tangent drawn from an external point P to a circle with centre O, QOR is the diameter of the circle. If ∠POR = 120°, what is the measure of ∠OPQ?
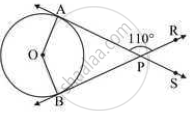
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 110°.
In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.

Construct a pair of tangents to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
The angle between two tangents to a circle may be 0°.
The length of tangent from an external point P on a circle with centre O is always less than OP.
In the given figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q meet at a point T. Find the length of TP.

From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents.
