Advertisements
Advertisements
प्रश्न
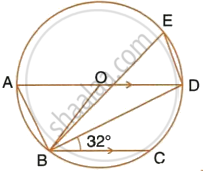
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
Find:
- ∠OBD
- ∠AOB
- ∠BED
उत्तर
i. AD is parallel to BC, i.e., OD is parallel to BC and BD is transversal
`=>` ∠ODB = ∠CBD = 32° ...(Alternate angles)
In ΔOBD,
OD = OB ...(Radii of the same circle)
`=>` ∠ODB = ∠OBD = 32°
ii. AD is parallel to BC, i.e., AO is parallel to BC and OB is transversal.
`=>` ∠AOB = ∠OBC ...(Alternate angles)
`=>` ∠OBC = ∠OBD + ∠DBC
`=>` ∠OBC = 32° + 32°
`=>` ∠OBC = 64°
`=>` ∠AOB = 64°
iii. In ΔOAB,
OA = OB ...(Radii of the same circle)
`=>` ∠OAB = ∠OBA = x ...(say)
`=>` ∠OAB + ∠OBA + ∠AOB = 180°
`=>` x + x + 64° = 180°
`=>` 2x = 180° – 64°
`=>` 2x = 116°
`=>` x = 58°
`=>` ∠OAB = 58°
i.e. ∠DAB = 58°
`=>` ∠DAB = ∠BED = 58° ...(Angles inscribed in the same arc are equal)
APPEARS IN
संबंधित प्रश्न
Prove that “The lengths of the two tangent segments to a circle drawn from an external point are equal.”
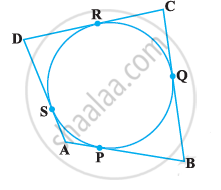
In the following Fig, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact to the centre.
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is ______.
In the following figure, PQ = QR, ∠RQP = 68°, PC and CQ are tangents to the circle with centre O.

Calculate the values of:
- ∠QOP
- ∠QCP
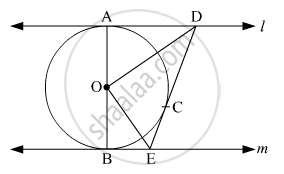
In fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that ∠DOE = 90° ?
In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
Prove that the lengths of two tangent segments drawn to the circle from an external point are equal.
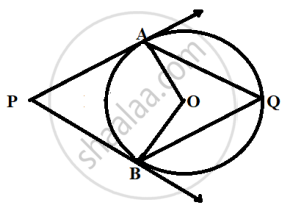
In the given figure, O is the centre of circle. Find ∠AQB, given that PA and PB are tangents to the circle and ∠APB = 75°.