Advertisements
Advertisements
प्रश्न
In the following figure, PQ = QR, ∠RQP = 68°, PC and CQ are tangents to the circle with centre O.

Calculate the values of:
- ∠QOP
- ∠QCP
उत्तर
In the figure, PQ = QR ∠RQP = 68°
PC and QC are tangents to the circle with centre O from C.
In ∠PQR,
PQ = QR ...(Given)
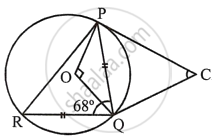
∴ ∠PRQ = ∠RPQ
But ∠PRQ + ∠RPQ + ∠RQP = 180° ...(Sum of angles of a triangle)
`\implies` ∠PRQ + ∠PRQ + 68° = 180°
`\implies` 2∠PRQ = 180° – 68° = 112°
∴ `∠PRQ = 112^circ/2 = 56^circ`
Now QC is tangent and PQ is chord
`\implies` ∠PQC = ∠PRQ = 56°
But ∠PQC = ∠QPC ...(∵ PC = QC tangents from C)
∴ ∠QPC = 56°
In ΔPQC,
∠C + ∠PQC + ∠QPC = 180° ...(Angles of a triangle)
∠C + 56° + 56° = 180°
`\implies` ∠C + 112° = 180°
`\implies` ∠C = 180° – 112° = 68°
But ∠POQ + ∠C = 180°
∴ ∠POQ + 68° = 180°
∴ ∠POQ = 180° – 68° = 112°
Hence ∠QOP = 112° and ∠QCP = 68°
APPEARS IN
संबंधित प्रश्न
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 50°, find ∠MQN.

Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
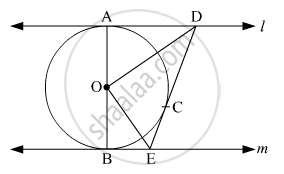
In fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that ∠DOE = 90° ?
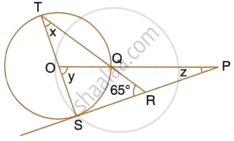
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and Z.
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
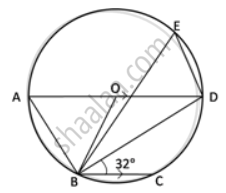
Find: ∠BED
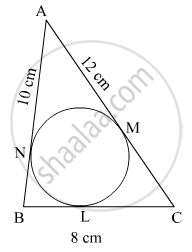
In Fig. 4, a circle is inscribed in a ΔABC having sides BC = 8 cm, AB = 10 cm and AC = 12 cm. Find the lengths BL, CM and AN.
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = `asqrt(2)`.
In the given figure, there are two concentric circles with centre O. If ARC and AQB are tangents to the smaller circle from the point A lying on the larger circle, find the length of AC, if AQ = 5 cm.

Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
Two concentric circles with centre O are of radii 3 cm and 5 cm. Find the length of chord AB of the larger circle which touches the smaller circle at P.

