Advertisements
Advertisements
प्रश्न
In the following figure, PQ = QR, ∠RQP = 68°, PC and CQ are tangents to the circle with centre O.

Calculate the values of:
- ∠QOP
- ∠QCP
उत्तर
In the figure, PQ = QR ∠RQP = 68°
PC and QC are tangents to the circle with centre O from C.
In ∠PQR,
PQ = QR ...(Given)
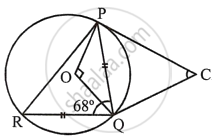
∴ ∠PRQ = ∠RPQ
But ∠PRQ + ∠RPQ + ∠RQP = 180° ...(Sum of angles of a triangle)
`\implies` ∠PRQ + ∠PRQ + 68° = 180°
`\implies` 2∠PRQ = 180° – 68° = 112°
∴ `∠PRQ = 112^circ/2 = 56^circ`
Now QC is tangent and PQ is chord
`\implies` ∠PQC = ∠PRQ = 56°
But ∠PQC = ∠QPC ...(∵ PC = QC tangents from C)
∴ ∠QPC = 56°
In ΔPQC,
∠C + ∠PQC + ∠QPC = 180° ...(Angles of a triangle)
∠C + 56° + 56° = 180°
`\implies` ∠C + 112° = 180°
`\implies` ∠C = 180° – 112° = 68°
But ∠POQ + ∠C = 180°
∴ ∠POQ + 68° = 180°
∴ ∠POQ = 180° – 68° = 112°
Hence ∠QOP = 112° and ∠QCP = 68°
APPEARS IN
संबंधित प्रश्न
From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
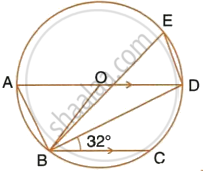
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
Find:
- ∠OBD
- ∠AOB
- ∠BED
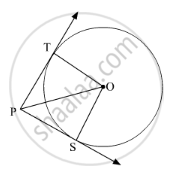
In Fig. 2, from a point P, two tangents PT and PS are drawn to a circle with centre O such that ∠SPT = 120°, Prove that OP = 2PS ?
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm the length of each tangent is equal to ______
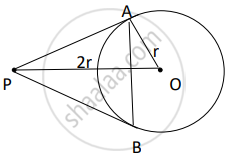
From a point P, two tangents PA and PB are drawn to a circle C(0, r). If OP = 2r, then find ∠APB. What type of triangle is APB?
In the given figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q meet at a point T. Find the length of TP.

PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ∠APB = 2∠OAB.

