Advertisements
Advertisements
प्रश्न
PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ∠APB = 2∠OAB.

उत्तर
Let ∠APB = x
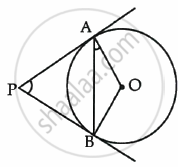
Now by theorem, the lengths of a tangents drawn from an external point to a circle are equal
So, PAB is an isosceles triangie
Therefore, ∠PAB = ∠PBA
= `1/2(180^circ - x)`
= `90^circ - x/2`
Also by theorem, the tangents at any point of a circle is perpendicular to the radius through the point of contact ∠OPT = 90°
Therefore, ∠OAB = ∠OAP – ∠PAB
= `90^circ - (90^circ - x/2)`
= `x/2`
= `1/2` ∠APB
Hence, ∠APB = 2∠OAB.
APPEARS IN
संबंधित प्रश्न
Prove that “The lengths of the two tangent segments to a circle drawn from an external point are equal.”
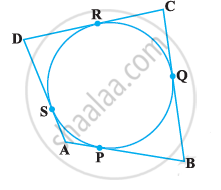
In the following Fig, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
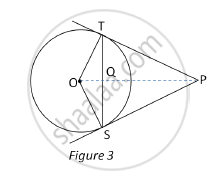
In Fig.3, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠ OTS = ∠ OST = 30°.
If from an external point P of a circle with centre O, two tangents PQ and PR are drawn such that ∠QPR = 120°, prove that 2PQ = PO.
Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
Prove that the lengths of two tangent segments drawn to the circle from an external point are equal.
The length of tangents drawn from an external point to the circle ______
In a circle of radius 17 cm, two parallel chords are drawn on opposite sides of a diameter. The distance between the chords is 23 cm. If the length of one chord is 16 cm, then the length of the other is ______
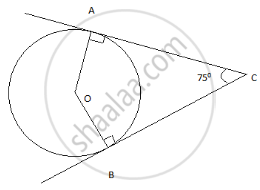
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB = ______
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
