Advertisements
Advertisements
प्रश्न
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
उत्तर
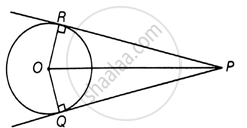
Given: Two tangents PQ and PR are drawn from an external point to a circle with centre O.
To Prove: QORP is a cyclic quadrilateral.
Proof: Since, PR and PQ are tangents.
So, OR ⊥ PR and OQ ⊥ PQ ...[Since, if we drawn a line from centre of a circle to its tangent line. Then, the line always perpendicular to the tangent line]
∴ ∠ORP = ∠OQP = 90°
Hence, ∠ORP + ∠OQP = 180°
So, QOPR is cyclic quadrilateral. ...[If sum of opposite angles is quadrilateral in 180°, then the quadrilateral is cyclic]
Hence proved.
APPEARS IN
संबंधित प्रश्न
Prove that “The lengths of the two tangent segments to a circle drawn from an external point are equal.”
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
In the following figure, PQ = QR, ∠RQP = 68°, PC and CQ are tangents to the circle with centre O.

Calculate the values of:
- ∠QOP
- ∠QCP
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
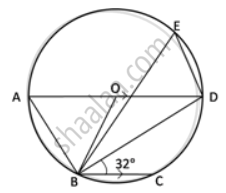
Find: ∠BED
Construct a pair of tangents to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm the length of each tangent is equal to ______
The number of tangents drawn at a point of the circle is/are ______
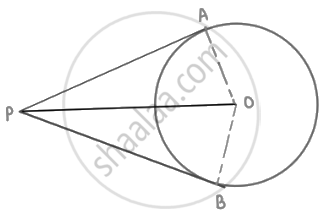
PA and PB are the two tangents drawn to the circle. O is the centre of the circle. A and B are the points of contact of the tangents PA and PB with the circle. If ∠OPA = 35°, then ∠POB = ______
In figure, common tangents AB and CD to two circles intersect at E. Prove that AB = CD.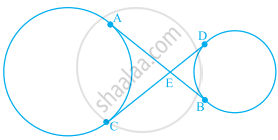
In the given figure, there are two concentric circles with centre O. If ARC and AQB are tangents to the smaller circle from the point A lying on the larger circle, find the length of AC, if AQ = 5 cm.

