Advertisements
Advertisements
प्रश्न
If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm the length of each tangent is equal to ______
विकल्प
`(3sqrt(3))/2 ` cm
6 cm
3 cm
`3sqrt(3)` cm
उत्तर
If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm the length of each tangent is equal to `underlinebb(3sqrt(3) cm)`.
Explanation:
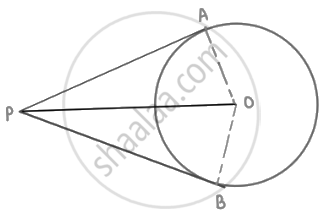
Let P be an external point from which pair of tangents are drawn as shown in the figure given below:
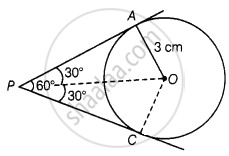
Join OA and OP
Also, OP is a bisector line of ∠APC.
∠APO = ∠CPO = 30°
OA ⊥ AP
Therefore, in triangle OAP
tan 30° = `"OA"/"AP"`
`1/sqrt3 = 3/"AP"`
AP = `3sqrt3` cm
संबंधित प्रश्न
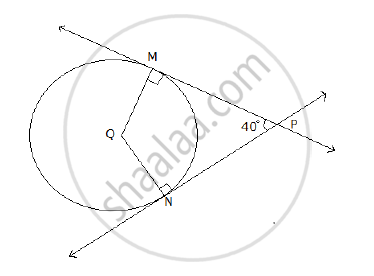
In the following figure, Q is the center of the circle. PM and PN are tangents to the circle. If ∠MPN = 40° , find ∠MQN.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
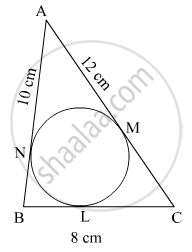
In Fig. 4, a circle is inscribed in a ΔABC having sides BC = 8 cm, AB = 10 cm and AC = 12 cm. Find the lengths BL, CM and AN.
PA and PB are the two tangents drawn to the circle. O is the centre of the circle. A and B are the points of contact of the tangents PA and PB with the circle. If ∠OPA = 35°, then ∠POB = ______
The angle between two tangents to a circle may be 0°.
The length of tangent from an external point P on a circle with centre O is always less than OP.
In figure, common tangents AB and CD to two circles intersect at E. Prove that AB = CD.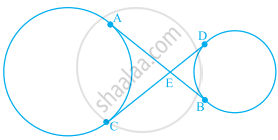
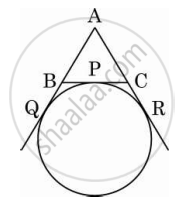
If a circle is touching the side BC of ΔABC at P and is touching AB and AC produced at Q and R respectively (see the figure). Prove that AQ = `1/2` (perimeter of ΔABC).
From a point P, the length of the tangent to a circle is 24 cm and the distance of P from the centre of the circle is 25 cm. Find the radius of the circle.
PA and PB are tangents drawn to a circle of centre O from an external point P. Chord AB makes an angle of 30° with the radius at the point of contact. If length of the chord is 6 cm, find the length of the tangent PA and the length of the radius OA.