Advertisements
Advertisements
Question
If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm the length of each tangent is equal to ______
Options
`(3sqrt(3))/2 ` cm
6 cm
3 cm
`3sqrt(3)` cm
Solution
If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm the length of each tangent is equal to `underlinebb(3sqrt(3) cm)`.
Explanation:
Let P be an external point from which pair of tangents are drawn as shown in the figure given below:
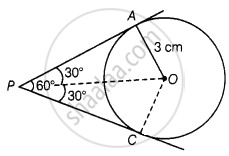
Join OA and OP
Also, OP is a bisector line of ∠APC.
∠APO = ∠CPO = 30°
OA ⊥ AP
Therefore, in triangle OAP
tan 30° = `"OA"/"AP"`
`1/sqrt3 = 3/"AP"`
AP = `3sqrt3` cm
RELATED QUESTIONS
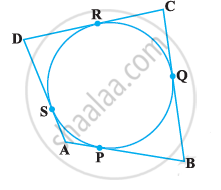
In the following Fig, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
In the given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is ______

Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the the perimeter of the triangle PCD.
Draw two concentric circles of radii 2 cm and 3 cm. From a point on the outer circle, construct a pair of tangents to the inner circle.
In the given diagram, O is the centre of the circle. PR and PT are two tangents drawn from the external point P and touching the circle at Q and S respectively. MN is a diameter of the circle. Given ∠PQM = 42° and ∠PSM = 25°.
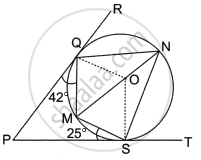
Find:
- ∠OQM
- ∠QNS
- ∠QOS
- ∠QMS
