Advertisements
Advertisements
Question
In the given diagram, O is the centre of the circle. PR and PT are two tangents drawn from the external point P and touching the circle at Q and S respectively. MN is a diameter of the circle. Given ∠PQM = 42° and ∠PSM = 25°.
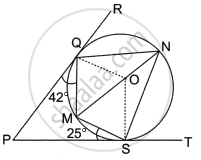
Find:
- ∠OQM
- ∠QNS
- ∠QOS
- ∠QMS
Solution
a. PR and PT are tangents to the circle with centre O.
Then, ∠OQP = 90°
As, radius is ⊥ to the tangent
Then, ∠OQM = ∠OQP – ∠MQP
= 90° – 42°
= 48°
b. ∠PQM = ∠QNM = 42° ...(By alternate segment theorem)
∠PSM = ∠SNM = 25°
Then ∠QNS = ∠QNM + ∠SNM
= 42° + 25°
= 67°
c. ∠QOS = 2∠QNS ...(since, angle subtended by the arc at the centre is twice the angle subtended by the arc at any other point of the circles.)
= 2 × 67°
= 134°
d. QNSN is a cyclic quadritateral
∠QNS + ∠QMS = 180°
∠QMS = 180° – 67° = 113°
APPEARS IN
RELATED QUESTIONS
Prove that “The lengths of the two tangent segments to a circle drawn from an external point are equal.”
Prove that a parallelogram circumscribing a circle is a rhombus.
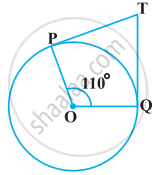
In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to ______.
Find the area of the shaded region in Fig. 8, where \\

In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

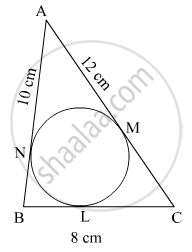
In Fig. 4, a circle is inscribed in a ΔABC having sides BC = 8 cm, AB = 10 cm and AC = 12 cm. Find the lengths BL, CM and AN.
The length of the tangent from an external point P on a circle with centre O is ______
In a circle of radius 17 cm, two parallel chords are drawn on opposite sides of a diameter. The distance between the chords is 23 cm. If the length of one chord is 16 cm, then the length of the other is ______
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BC.
In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.

