Advertisements
Advertisements
Question
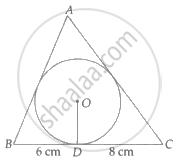
In Fig. 4, a circle is inscribed in a ΔABC having sides BC = 8 cm, AB = 10 cm and AC = 12 cm. Find the lengths BL, CM and AN.
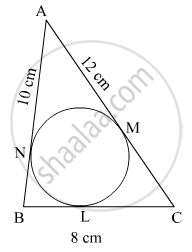
Solution
BN and BL are tangents from the same point to the circle
∴ BN = BL
Similarly
AM = AN and CL = CM
Given that
AB = 10 cm, BC = 8 cm and AC = 12 cm
Let
AN = AM = x
CM = CL = y
BN = BL = z
AB + AN + NB = 10
BC = BL + LC = 8
AC = AM + MC
=
Adding equations (1), (2) and (3), we get
2 (x + y + z) = 30
⇒ x + y + z = 15 ...(4)
Subtracting (1) from (4) we get
y = 5
Subtracting (2) from (4) we get
x = 7
Subtracting (3) from (4) we get
z = 3
BL = z = 3 cm
CM = y = 5 cm
AN = x = 7 cm
APPEARS IN
RELATED QUESTIONS
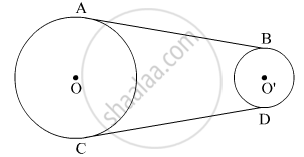
In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.
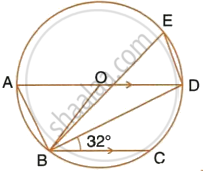
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
Find:
- ∠OBD
- ∠AOB
- ∠BED
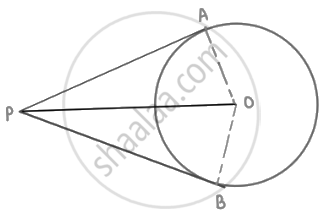
PA and PB are the two tangents drawn to the circle. O is the centre of the circle. A and B are the points of contact of the tangents PA and PB with the circle. If ∠OPA = 35°, then ∠POB = ______
In the given figure, there are two concentric circles with centre O. If ARC and AQB are tangents to the smaller circle from the point A lying on the larger circle, find the length of AC, if AQ = 5 cm.

In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 6 cm and 8 cm respectively. If the area of ΔABC is 84 cm2, find the lengths of sides AB and AC.
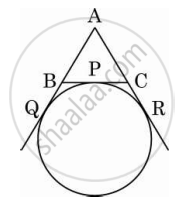
If a circle is touching the side BC of ΔABC at P and is touching AB and AC produced at Q and R respectively (see the figure). Prove that AQ =
In the given figure, PA and PB are tangents from external point P to a circle with centre C and Q is any point on the circle. Then the measure of ∠AQB is ______.

Two concentric circles with centre O are of radii 3 cm and 5 cm. Find the length of chord AB of the larger circle which touches the smaller circle at P.

From a point P, the length of the tangent to a circle is 24 cm and the distance of P from the centre of the circle is 25 cm. Find the radius of the circle.
In the given diagram, O is the centre of the circle. PR and PT are two tangents drawn from the external point P and touching the circle at Q and S respectively. MN is a diameter of the circle. Given ∠PQM = 42° and ∠PSM = 25°.
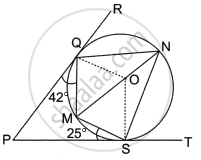
Find:
- ∠OQM
- ∠QNS
- ∠QOS
- ∠QMS
