Advertisements
Advertisements
प्रश्न
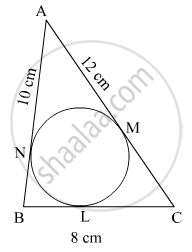
In Fig. 4, a circle is inscribed in a ΔABC having sides BC = 8 cm, AB = 10 cm and AC = 12 cm. Find the lengths BL, CM and AN.
उत्तर
BN and BL are tangents from the same point to the circle
∴ BN = BL
Similarly
AM = AN and CL = CM
Given that
AB = 10 cm, BC = 8 cm and AC = 12 cm
Let
AN = AM = x
CM = CL = y
BN = BL = z
AB + AN + NB = 10
`x + z = 10` ...(1)
BC = BL + LC = 8
`z + y = 8` ...(2)
AC = AM + MC
= `x + y = 12` ...(3)
Adding equations (1), (2) and (3), we get
2 (x + y + z) = 30
⇒ x + y + z = 15 ...(4)
Subtracting (1) from (4) we get
y = 5
Subtracting (2) from (4) we get
x = 7
Subtracting (3) from (4) we get
z = 3
BL = z = 3 cm
CM = y = 5 cm
AN = x = 7 cm
APPEARS IN
संबंधित प्रश्न
Prove that the lengths of the tangents drawn from an external point to a circle are equal.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other an angle of 80°, then ∠POA is equal to ______.
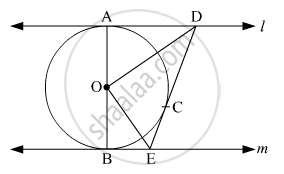
In fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that ∠DOE = 90° ?
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
In the given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is ______

The length of the tangent from an external point P on a circle with centre O is ______
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BC.
In the given figure, if a circle touches the side QR of ΔPQR at S and extended sides PQ and PR at M and N, respectively, then prove that PM = `1/2` (PQ + QR + PR)
In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.

