Advertisements
Advertisements
प्रश्न
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

उत्तर
In a cyclic quadrilateral ABCD,
`∠ ABC+∠ADC=180°` (Opposite angle of a cydic quadrilateral are supplementary)
`⇒ 100°+∠ADC=180°`
`⇒ ∠ADC=80°`
Now, in `ΔACD`,
`∠ADC+∠CAD+∠ADC=180°`
`⇒40°+∠CAD+80°=180°`
`⇒∠CAD=180°-120°`
`⇒∠CAD=60°`
`"Now" ∠DCT=∠CAD ...........("angles in the alternate segment are equal")`
`∴ ∠DCT=60°`
APPEARS IN
संबंधित प्रश्न
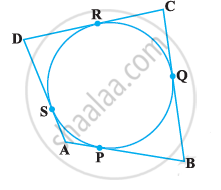
In the following Fig, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
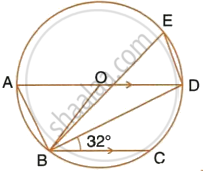
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
Find:
- ∠OBD
- ∠AOB
- ∠BED
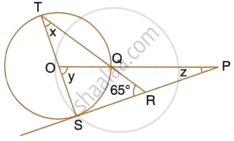
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and Z.
In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.

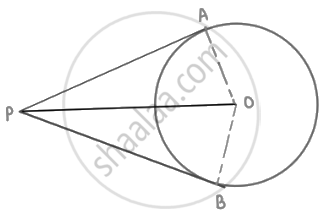
PA and PB are the two tangents drawn to the circle. O is the centre of the circle. A and B are the points of contact of the tangents PA and PB with the circle. If ∠OPA = 35°, then ∠POB = ______
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
Draw two concentric circles of radii 2 cm and 3 cm. From a point on the outer circle, construct a pair of tangents to the inner circle.
In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.

Two concentric circles with centre O are of radii 3 cm and 5 cm. Find the length of chord AB of the larger circle which touches the smaller circle at P.

