Advertisements
Advertisements
प्रश्न
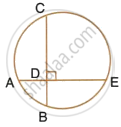
In the given figure, AE and BC intersect each other as point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find AE.
उत्तर
In the given circle,
Chords AE and BC intersect each other at D at right angle i.e., ∠CDE = 90°, AB is joined AB = 5 cm, BD = 4 cm, CD = 9 cm
Now we have to find AE.
Let DE = x m
Now in right ΔABD,
AB2 = AD2 + BD2 ...(Pythagoras Theorem)
`\implies` (5)2 = AD2 + (4)2
`\implies` 25 = AD2 + 16
`\implies` AD2 = 25 – 16 = 9 = (3)2
∴ AD = 3 cm
∵ Chords AE and BC intersect each other at D inside the circle
∴ AD × DE = BD × DC
`\implies` 3 × x = 4 × 9
`\implies x = (4 xx 9)/3 = 12 cm`
`\implies` DE = 12 cm
∴ AE = AD + DE
= 3 + 12
= 15 cm
APPEARS IN
संबंधित प्रश्न
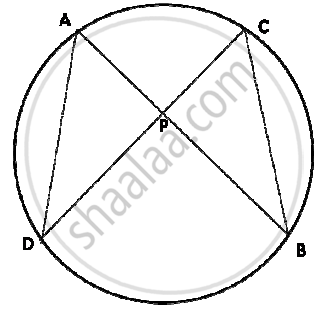
AB and CD are two chords of a circle intersecting at P. Prove that AP x PB = CP x PD
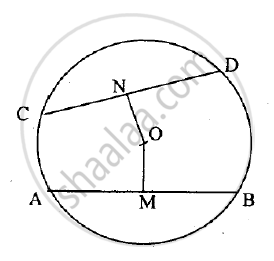
In the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD.
AB = 24 cm, OM= 5 cm, ON= 12 cm. Find the:
1) radius of the circle
2) length of chord CD.
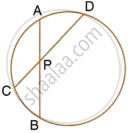
In the given figure 3 × CP = PD = 9 cm and AP = 4.5 cm. Find BP.
In the given figure, 5 × PA = 3 × AB = 30 cm and PC = 4 cm. Find CD.
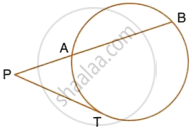
In the given figure, tangent PT = 12.5 cm and PA = 10 cm; find AB.
Prove that, of any two chords of a circle, the greater chord is nearer to the centre.
Chords AB and CD of a circle intersect each other at point P such that AP = CP
Show that: AB = CD
Two tangents are drawn to a circle from an external point P. touching the circle at the points A and B. A third tangent intersects segment PA in C and segment PB in D and touches the circle at Q. if PA = 20 units, find the perimeter of Δ PCD.
If AB and CD are two chords which when produced meet at P and if AP = CP, show that AB = CD.
Two circles of radii 10 cm and 8 cm intersect and the length of the common chord is 12 cm. Find the distance between their centres.
