Advertisements
Advertisements
प्रश्न
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
उत्तर
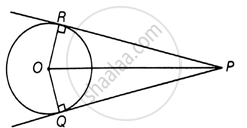
Given: Two tangents PQ and PR are drawn from an external point to a circle with centre O.
To Prove: QORP is a cyclic quadrilateral.
Proof: Since, PR and PQ are tangents.
So, OR ⊥ PR and OQ ⊥ PQ ...[Since, if we drawn a line from centre of a circle to its tangent line. Then, the line always perpendicular to the tangent line]
∴ ∠ORP = ∠OQP = 90°
Hence, ∠ORP + ∠OQP = 180°
So, QOPR is cyclic quadrilateral. ...[If sum of opposite angles is quadrilateral in 180°, then the quadrilateral is cyclic]
Hence proved.
APPEARS IN
संबंधित प्रश्न
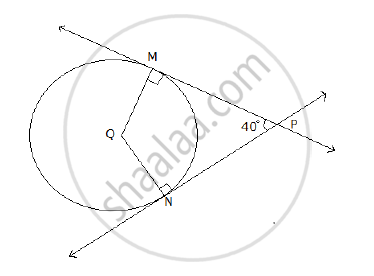
In the following figure, Q is the center of the circle. PM and PN are tangents to the circle. If ∠MPN = 40° , find ∠MQN.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
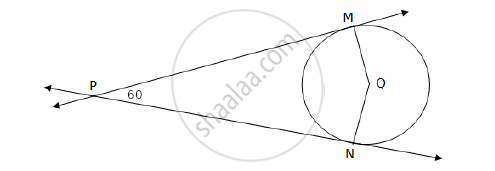
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 60°, find ∠MQN.
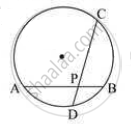
In the given figure PA = 6, PB = 4 and PC = 8. Find PD
In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.

The length of a tangent drawn from a point at a distance of 10 cm of the circle is 8 cm. The radius of the circle is ______
The length of the tangent from an external point on a circle is ______
In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.

Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
