Advertisements
Advertisements
प्रश्न
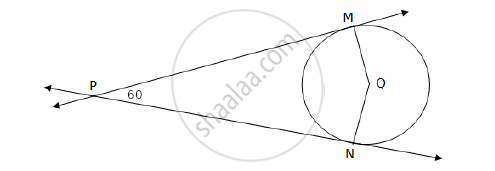
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 60°, find ∠MQN.
उत्तर

Seg PM and seg PN are tangents to the circle and seg QM and seg QN are the radii from the points of contacts.
m∠PMQ = m∠PNQ = 90° ... (Tangent is perpendicular to the radius) ... (1)
The sum of the measures of the angles of a quadrilateral is 360°.
m∠MPN + m∠PMQ + m∠MQN + m∠PNQ = 360°
60° + 90° + m∠MQN + 90° = 360°
240° + m∠MQN = 360°
m∠MQN = 360° – 240° = 120° ... [From (1)]
APPEARS IN
संबंधित प्रश्न
In the below given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If∠PRQ = 120°, then prove that OR = PR + RQ.

Prove that a parallelogram circumscribing a circle is a rhombus.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other an angle of 80°, then ∠POA is equal to ______.
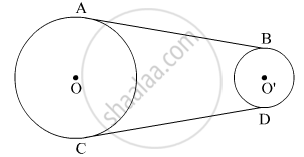
In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.
PQ is a tangent drawn from an external point P to a circle with centre O, QOR is the diameter of the circle. If ∠POR = 120°, what is the measure of ∠OPQ?
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

Find: ∠AOB
If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm the length of each tangent is equal to ______
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = `asqrt(2)`.
The length of tangent from an external point P on a circle with centre O is always less than OP.
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
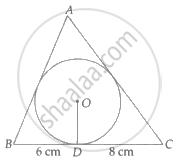
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 6 cm and 8 cm respectively. If the area of ΔABC is 84 cm2, find the lengths of sides AB and AC.
In the given figure, PA and PB are tangents from external point P to a circle with centre C and Q is any point on the circle. Then the measure of ∠AQB is ______.

From a point P, the length of the tangent to a circle is 24 cm and the distance of P from the centre of the circle is 25 cm. Find the radius of the circle.
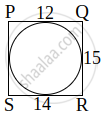
A quadrilateral PQRS is drawn to circumscribe a circle. If PQ = 12 cm, QR = 15 cm and RS = 14 cm, then find the length of SP is ______.
In the given diagram, O is the centre of the circle. PR and PT are two tangents drawn from the external point P and touching the circle at Q and S respectively. MN is a diameter of the circle. Given ∠PQM = 42° and ∠PSM = 25°.
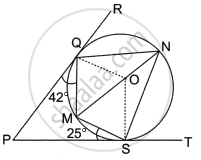
Find:
- ∠OQM
- ∠QNS
- ∠QOS
- ∠QMS
