Advertisements
Advertisements
प्रश्न
In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.
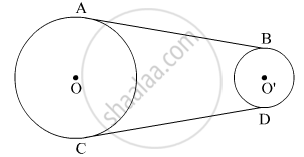
उत्तर १
Construct a line passing through AD
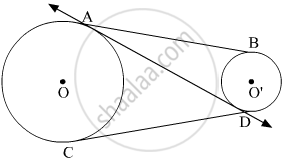
Now, AD and CD are tangents to the circle with centre O from the external point D.
So, AD = CD (Tangents drawn from an external point to a circle are equal) ...(1)
Also, AB and AD are the tangents to the circle with centre O' from the external point A.
So, AD = AB (Tangents drawn from an external point to a circle are equal) ...(2)
From (1) and (2)
AB = CD
Hence proved.
उत्तर २
Given: AB and CD are two common tangents to two circles of unequal radii.
To Prove: AB = CD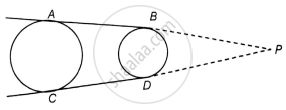
Construction: Produce AB and CD, to intersect at P.
Proof: Consider the circle with greater radius.
AP = CP ...[Tangents drawn from an external point to a circle are equal] [1]
Also, Consider the circle with smaller radius.
BP = BD ...[Tangents drawn from an external point to a circle are equal] [2]
Substract [2] from [1], we get
AP – BP = CP – BD
AB = CD
Hence proved.
संबंधित प्रश्न
Prove that “The lengths of the two tangent segments to a circle drawn from an external point are equal.”
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact to the centre.
In the given figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°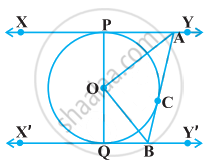
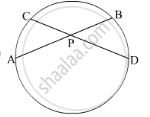
In the given figure PA = 10, PB = 2 and PC = 5. Find PD.
A right circular cone is divided into three parts by trisecting its height by two planes drawn parallel to the base. Show that the volumes of the three portions starting from the top are in the ratio 1 : 7 : 19 ?
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

Find: ∠AOB
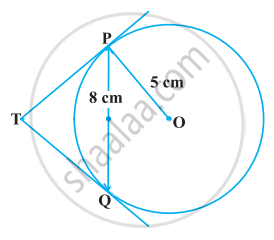
ln Figure, PQ is a chord of length 8 cm of a circle of radius 5 cm and centre O. The tangents at P and Q intersect at point T. find the length of TP.
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
The length of the tangent from an external point on a circle is ______
In the given figure, O is the centre of circle. Find ∠AQB, given that PA and PB are tangents to the circle and ∠APB = 75°.