Advertisements
Advertisements
प्रश्न
A right circular cone is divided into three parts by trisecting its height by two planes drawn parallel to the base. Show that the volumes of the three portions starting from the top are in the ratio 1 : 7 : 19 ?
उत्तर
Let ABC be a right circular cone of height 3h and base radius r. This cone is cut by two planes such that AQ = QP = PO = h.
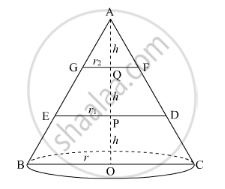
Since
\[ \Rightarrow \frac{3h}{2h} = \frac{r}{r_1}\]
\[ \Rightarrow r_1 = \frac{2r}{3} . . . . . \left( 1 \right)\]
Also,
\[ \Rightarrow \frac{3h}{h} = \frac{r}{r_2}\]
\[ \Rightarrow r_2 = \frac{r}{3} . . . . . \left( 2 \right)\]
Voulme of cone AGF,
\[V_1 = \frac{1}{3}\pi {r_2}^2 h\]
\[ = \frac{1}{3}\pi \left( \frac{r}{3} \right)^2 h \left[ From \left( 2 \right) \right]\]
\[ = \frac{1}{27}\pi r^2 h\]
Voulme of the frustum GFDE,
\[V_2 = \frac{1}{3}\pi\left( {r_1}^2 + {r_2}^2 + r_1 r_2 \right)h\]
\[ = \frac{1}{3}\pi\left( \frac{4 r^2}{9} + \frac{r^2}{9} + \frac{2 r^2}{9} \right)h \left[ From \left( 1 \right) and \left( 2 \right) \right]\]
\[ = \frac{7}{27}\pi r^2 h\]
Voulme of the frustum EDCB,
\[V_3 = \frac{1}{3}\pi\left( r^2 + {r_1}^2 + r_1 r \right)h\]
\[ = \frac{1}{3}\pi\left( r^2 + \frac{4 r^2}{9} + \frac{2 r^2}{3} \right)h \left[ From \left( 1 \right) and \left( 2 \right) \right]\]
\[ = \frac{19}{27}\pi r^2 h\]
∴ Required ratio =\[V_1 : V_2 : V_3 = \frac{1}{27}\pi r^2 h: \frac{7}{27}\pi r^2 h: \frac{19}{27}\pi r^2 h = 1: 7: 19\]
APPEARS IN
संबंधित प्रश्न
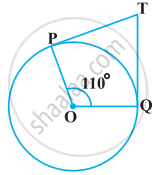
In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to ______.
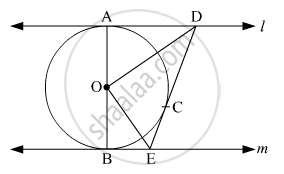
In fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that ∠DOE = 90° ?
If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm the length of each tangent is equal to ______
In the given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is ______

The angle between two tangents to a circle may be 0°.
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = `asqrt(2)`.
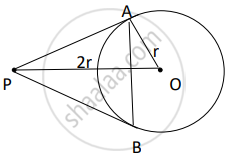
From a point P, two tangents PA and PB are drawn to a circle C(0, r). If OP = 2r, then find ∠APB. What type of triangle is APB?
In the given figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q meet at a point T. Find the length of TP.

If a circle is touching the side BC of ΔABC at P and is touching AB and AC produced at Q and R respectively (see the figure). Prove that AQ = `1/2` (perimeter of ΔABC).
From a point P, the length of the tangent to a circle is 24 cm and the distance of P from the centre of the circle is 25 cm. Find the radius of the circle.
