Advertisements
Advertisements
प्रश्न
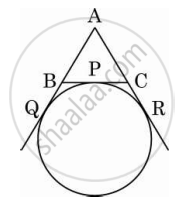
If a circle is touching the side BC of ΔABC at P and is touching AB and AC produced at Q and R respectively (see the figure). Prove that AQ = `1/2` (perimeter of ΔABC).
उत्तर
Given, circle touching the side BC of ΔABC at point P and AB, AC produced at Q and R, respectively.
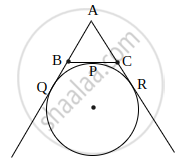
We know, lengths of tangents drawn from on external point to a circle are equal.
∴ AQ = AR ...(i)
BQ = BP ...(ii)
CP = CR ...(iii)
Perimeter of ΔABC = AB + BC + CA
=AB + (BP + PC) + (AR – CR)
= (AB + BP) + PC + (AQ – CP) ...[From equations (i) and (ii)]
= (AB + BQ) + PC + (AQ – CP) ...[From equation (ii)]
= AQ + PC + AQ – PC
= 2AQ
∴ AQ = `1/2` (perimeter of ΔABC)
APPEARS IN
संबंधित प्रश्न
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 50°, find ∠MQN.

Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact to the centre.
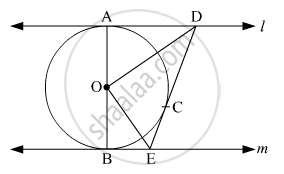
In fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that ∠DOE = 90° ?
Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
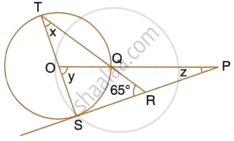
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and Z.
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
In figure, common tangents AB and CD to two circles intersect at E. Prove that AB = CD.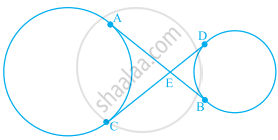
From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the the perimeter of the triangle PCD.
In the given figure, there are two concentric circles with centre O. If ARC and AQB are tangents to the smaller circle from the point A lying on the larger circle, find the length of AC, if AQ = 5 cm.

