Advertisements
Advertisements
प्रश्न
From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the the perimeter of the triangle PCD.
उत्तर
Two tangents PA and PB are drawn to a circle with centre O from an external point P

Perimeter of ΔPCD = PC + CD + PD
= PC + CE + ED + PD
= PC + CA + DB + PD
= PA + PB
= 2PA
= 2(10)
= 20 cm ...[∵ CE = CA, DE = DB, PA = PB tangents from internal point to a circle are equal]
संबंधित प्रश्न
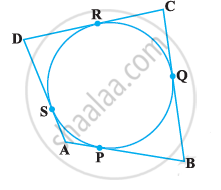
In the following Fig, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

Find: ∠AOB
In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.

In figure, common tangents AB and CD to two circles intersect at E. Prove that AB = CD.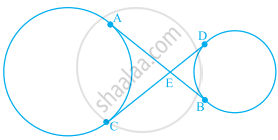
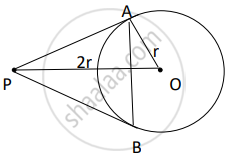
From a point P, two tangents PA and PB are drawn to a circle C(0, r). If OP = 2r, then find ∠APB. What type of triangle is APB?
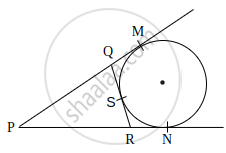
In the given figure, if a circle touches the side QR of ΔPQR at S and extended sides PQ and PR at M and N, respectively, then prove that PM = `1/2` (PQ + QR + PR)
In the given figure, perimeter of ΔPQR is 20 cm. Find the length of tangent PA.

Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
