Advertisements
Advertisements
प्रश्न
Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s – b.
उत्तर
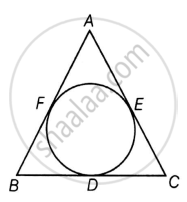
A triangle ABC with BC = a, CA = b and AB = c.
Also, a circle is inscribed, which touches the sides BC, CA and AB at D, E and F, respectively and s is semi-perimeter of the triangle
To Prove: BD = s – b
Proof:
We have,
Semi Perimeter = s
Perimeter = 2s
2s = AB + BC + AC ...[1]
As we know,
Tangents drawn from an external point to a circle are equal
So we have
AF = AE ...[2] [Tangents from point A]
BF = BD ...[3] [Tangents from point B]
CD = CE ...[4] [Tangents from point C]
Adding [2] [3] and [4]
AF + BF + CD = AE + BD + CE
AB + CD = AC + BD
Adding BD both side
AB + CD + BD = AC + BD + BD
AB + BC – AC = 2BD
AB + BC + AC – AC – AC = 2BD
2s – 2AC = 2BD ...[From 1]
2BD = 2s – 2b ...[As AC = b]
BD = s – b
Hence proved.
APPEARS IN
संबंधित प्रश्न
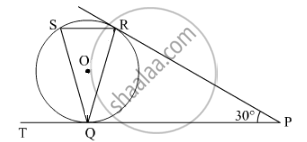
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
In the given figure, PQ is chord of a circle with centre O an PT is a tangent. If
∠QPT = 60°, find the ∠PRQ.

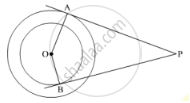
Tangents PA and PB are drawn from an external point P to two concentric circles with centre O and radii 8 cm and 5 cm respectively, as shown in Fig. 3. If AP = 15 cm, then find the length of BP.
If O is the centre of the circle, find the value of x in each of the following figures

Use the figure given below to fill in the blank:
Diameter of a circle is ______.

Use the figure given below to fill in the blank:
AB is a ______ of the circle.

Draw a circle of radius 6 cm. In the circle, draw a chord AB = 6 cm.
(i) If O is the center of the circle, join OA and OB.
(ii) Assign a special name to ∆AOB
(iii) Write the measure of angle AOB.
In a circle with centre P, chord AB is parallel to a tangent and intersects the radius drawn from the point of contact to its midpoint. If AB = `16sqrt(3)`, then find the radius of the circle
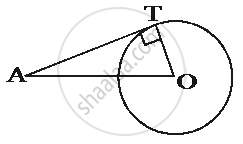
A point A is 26 cm away from the centre of a circle and the length of the tangent drawn from A to the circle is 24 cm. Find the radius of the circle.
From the figure, identify a sector.

