Advertisements
Advertisements
प्रश्न
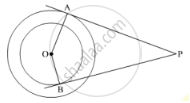
Tangents PA and PB are drawn from an external point P to two concentric circles with centre O and radii 8 cm and 5 cm respectively, as shown in Fig. 3. If AP = 15 cm, then find the length of BP.
उत्तर
To find: BP
Construction: Join OP.
`Now ,OA _|_AP`and `OB_|_BP` `[therefore\text{Tangent to a circle is prependicular to the radius through the point of contact}]`
⇒ ∠OAP = ∠OBP = 90°
On applying Pythagoras theorem in ΔOAP, we obtain:
(OP)2 = (OA)2 + (AP)2
⇒ (OP)2 = (8)2 + (15)2
⇒ (OP)2 = 64 + 225
⇒ (OP)2 = 289
`rArr OP=sqrt289`
⇒ OP = 17
Thus, the length of OP is 17 cm.
On applying Pythagoras theorem in ΔOBP, we obtain:
(OP)2= (OB)2 + (BP)2
⇒ (17)2 = (5)2 + (BP)2
⇒ 289 = 25 + (BP)2
⇒ (BP)2 = 289 − 25
⇒ (BP)2 = 264
⇒ BP = 16.25 cm (approx.)
Hence, the length of BP is 16.25 cm.
संबंधित प्रश्न
Fill in the blanks:
A point, whose distance from the centre of a circle is greater than its radius lies in __________ of the circle. (exterior/ interior)
In the following figure, AB is the diameter of a circle with centre O and CD is the chord with length equal to radius OA.
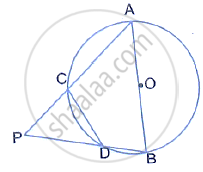
Is AC produced and BD produced meet at point P; show that ∠APB = 60°
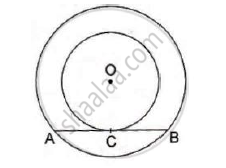
In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.
A circle is inscribed in a ΔABC touching AB, BC and AC at P, Q and R respectively. If AB = 10 cm, AR=7cm and CR=5cm, find the length of BC.

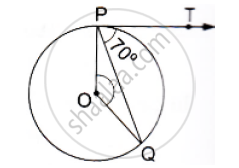
If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.
In the given figure, O is the centre of the circle. Find ∠CBD.

In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?
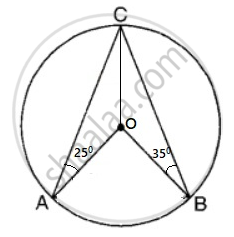
In the adjoining figure ‘O’ is the center of the circle, ∠CAO = 25° and ∠CBO = 35°. What is the value of ∠AOB?
If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°.
