Advertisements
Advertisements
प्रश्न
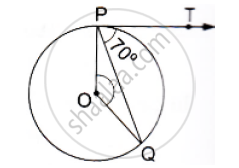
If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.
उत्तर
We know that the radius and tangent are perpendicular at their point of contact.
∴ ∠OPT = 90°
Now, ∠OPQ = ∠OPT - ∠TPQ = 90° -70° = 20°
Since, OP = OQ as both are radius
∴ ∠OPQ = ∠OQP = 20° (Angles opposite to equal sides are equal)
Now, In isosceles Δ POQ
∠POQ + ∠OPQ + ∠OQP = 180° (Angle sum property of a triangle)
⇒ ∠POQ =180° - 20° = 140°
APPEARS IN
संबंधित प्रश्न
Prove that the tangents at the extremities of any chord make equal angles with the chord.
In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.

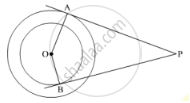
Tangents PA and PB are drawn from an external point P to two concentric circles with centre O and radii 8 cm and 5 cm respectively, as shown in Fig. 3. If AP = 15 cm, then find the length of BP.
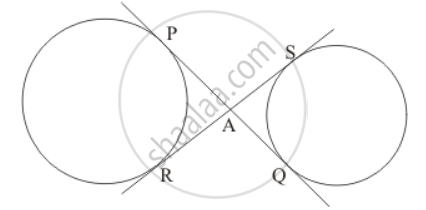
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
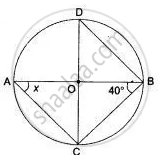
If O is the centre of the circle, find the value of x in each of the following figures
In the adjoining figure, seg DE is the chord of the circle with center C. seg CF⊥ seg DE and DE = 16 cm, then find the length of DF?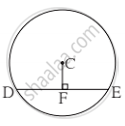
C(O, r1) and C(O, r2) are two concentric circles with r1 > r2 AB is a chord of C(O, r1) touching C(O, r2) at C then ______
If the angle between two radii of a circle is 130°, then the angle between the tangents at the ends of the radii is ______
If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is ______.
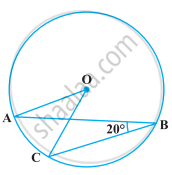
In the following figure, if ∠ABC = 20º, then ∠AOC is equal to ______.