Advertisements
Advertisements
प्रश्न
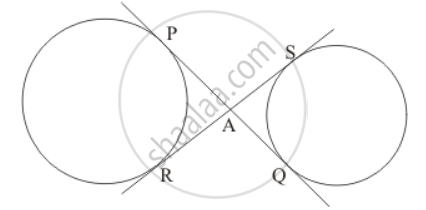
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
उत्तर
The figure given in the question is
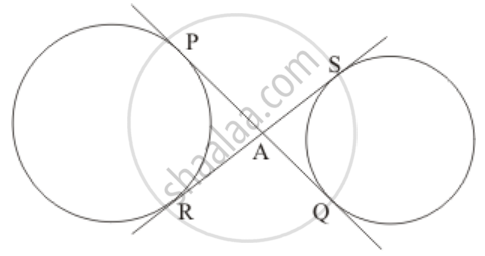
We know from the property of tangents that the length of two tangents drawn from a common external point will be equal. Therefore,
PA = RA …… (1)
AQ = AS …… (2)
Let us add equation (1) and (2)
PA + AQ = RA + AS
PQ = RS
Thus we have proved that PQ = RS.
APPEARS IN
संबंधित प्रश्न
Two circles touch each other externally at P. AB is a common tangent to the circles touching them at A and B. The value of ∠ L APB is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
Two tangent segments PA and PB are drawn to a circle with center O such that ∠APB =120°. Prove that OP = 2AP
Fill in the blank
A continuous piece of a circle is ............... of the circle
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BC and DC into which BC is divided by the point of contact D, are of
lengths 6cm and 9cm respectively. If the area of 2 ΔABC = 54cm2 then find the lengths of sides AB and AC.

PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.

State, if the following statement is true or false:
The longest chord of a circle is its diameter.
If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ.
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

From the figure, identify the centre of the circle.
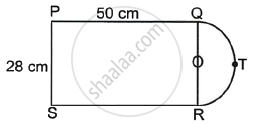
A figure is in the form of rectangle PQRS having a semi-circle on side QR as shown in the figure. Determine the area of the plot.