Advertisements
Advertisements
प्रश्न
Two concentric circles are of diameters 30 cm and 18 cm. Find the length of the chord of the larger circle which touches the smaller circle.
उत्तर
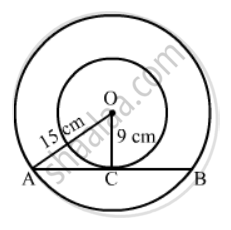
Let O be the common centre of the two circles and AB be the chord of the larger circle which touches the smaller circle at C.
Join OA and OC. Then,
OC = \[\frac{18}{2}\]
cm = 9 cm and OA =\[\frac{30}{2}\] cm = 15 cm
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact. Also, the perpendicular drawn from the centre of a circle to a chord bisects the chord.
∴ OC ⊥ AB and C is the mid-point of AB.
In right ∆OCA,
\[{OA}^2 = {OC}^2 + {AC}^2 \left( \text{Pythagoras theorem} \right)\]
\[ \Rightarrow {AC}^2 = {OA}^2 - {OC}^2 \]
\[ \Rightarrow AC = \sqrt{{15}^2 - 9^2}\]
\[ \Rightarrow AC = \sqrt{225 - 81} = \sqrt{144} = 12 cm\]
∴ AB = 2AC = 2 × 12 cm = 24 cm
Thus, the required length of the chord is 24 cm.
APPEARS IN
संबंधित प्रश्न
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

From an external point P , tangents PA = PB are drawn to a circle with centre O . If \[\angle PAB = {50}^o\] , then find \[\angle AOB\]
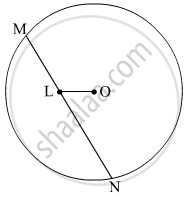
In the given figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
Draw circle with diameter: 8.4 cm
In above case, measure the length of the radius of the circle drawn.
A part of circumference of a circle is called as _______
Find the radius of the circle
Diameter = 24 cm
A line through the point of contact and passing through centre of the circle is known as ______
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is ______
