Advertisements
Advertisements
Question
Two concentric circles are of diameters 30 cm and 18 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution
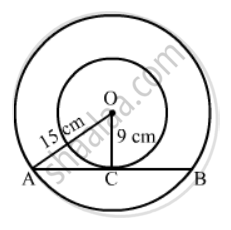
Let O be the common centre of the two circles and AB be the chord of the larger circle which touches the smaller circle at C.
Join OA and OC. Then,
OC = \[\frac{18}{2}\]
cm = 9 cm and OA =\[\frac{30}{2}\] cm = 15 cm
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact. Also, the perpendicular drawn from the centre of a circle to a chord bisects the chord.
∴ OC ⊥ AB and C is the mid-point of AB.
In right ∆OCA,
\[{OA}^2 = {OC}^2 + {AC}^2 \left( \text{Pythagoras theorem} \right)\]
\[ \Rightarrow {AC}^2 = {OA}^2 - {OC}^2 \]
\[ \Rightarrow AC = \sqrt{{15}^2 - 9^2}\]
\[ \Rightarrow AC = \sqrt{225 - 81} = \sqrt{144} = 12 cm\]
∴ AB = 2AC = 2 × 12 cm = 24 cm
Thus, the required length of the chord is 24 cm.
APPEARS IN
RELATED QUESTIONS
In the fig. a circle is inscribed in a quadrilateral ABCD in which ∠B = 90° if AD = 23cm,
AB = 29cm and DS = 5cm, find the radius of the circle.
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4cm and 3cm respectively. If the area of 2 ABC 21cm then find the lengths of sides AB and AC.
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.

The perimeter (in cm) of a square circumscribing a circle of radius a cm, is
Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
Draw a circle of any radius. Show one diameter, one radius and one chord on that circle.
Find the diameter of the circle
Radius = 10 cm
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, find ∠CBA see figure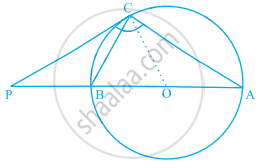
In the following figure, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.
From the figure, identify a segment.

