Advertisements
Advertisements
प्रश्न
Two concentric circles are of diameters 30 cm and 18 cm. Find the length of the chord of the larger circle which touches the smaller circle.
उत्तर
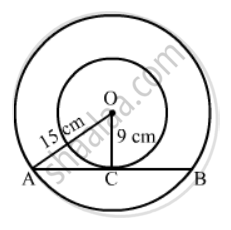
Let O be the common centre of the two circles and AB be the chord of the larger circle which touches the smaller circle at C.
Join OA and OC. Then,
OC = \[\frac{18}{2}\]
cm = 9 cm and OA =\[\frac{30}{2}\] cm = 15 cm
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact. Also, the perpendicular drawn from the centre of a circle to a chord bisects the chord.
∴ OC ⊥ AB and C is the mid-point of AB.
In right ∆OCA,
\[{OA}^2 = {OC}^2 + {AC}^2 \left( \text{Pythagoras theorem} \right)\]
\[ \Rightarrow {AC}^2 = {OA}^2 - {OC}^2 \]
\[ \Rightarrow AC = \sqrt{{15}^2 - 9^2}\]
\[ \Rightarrow AC = \sqrt{225 - 81} = \sqrt{144} = 12 cm\]
∴ AB = 2AC = 2 × 12 cm = 24 cm
Thus, the required length of the chord is 24 cm.
APPEARS IN
संबंधित प्रश्न
A circle touches the side BC of a ΔABC at a point P and touches AB and AC when produced at Q and R respectively. As shown in the figure that AQ = `1/2` (Perimeter of ΔABC).

In the adjoining figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB=6cm, BC=9cm and CD=8 cm. Find the length of side AD.
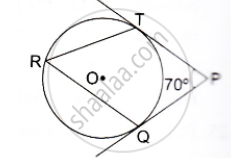
In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70° , find the ∠TRQ.
In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.
In the given figure, the area enclosed between the two concentric circles is 770 cm2. If the radius of the outer circle is 21 cm, calculate the radius of the inner circle.
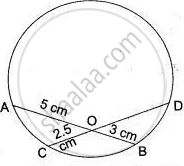
In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.
Draw circle with diameter: 6 cm
In above case, measure the length of the radius of the circle drawn.
Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of the common chord PQ.
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
