Advertisements
Advertisements
प्रश्न
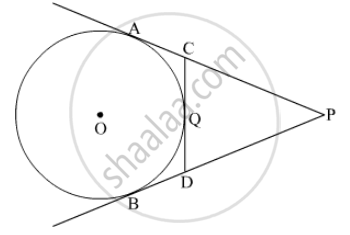
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.
उत्तर
Given: PA and PB are the tangents to the circle.
PA = 12 cm
QC = QD = 3 cm
To find: PC + PD
PA = PB = 12 cm (The lengths of tangents drawn from an external point to a circle are equal)
Similarly, QC = AC = 3 cm
and QD = BD = 3 cm.
Now, PC = PA − AC = 12 − 3 = 9 cm
Similarly, PD = PB − BD = 12 − 3 = 9 cm
Hence, PC + PD = 9 + 9 = 18 cm.
APPEARS IN
संबंधित प्रश्न
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
In two concentric circles, a chord of length 8 cm of the large circle touches the smaller circle. If the radius of the larger circle is 5 cm, then find the radius of the smaller circle.
In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

Use the figure given below to fill in the blank:
EF is a ______ of the circle.

Use the figure given below to fill in the blank:
______ is a chord of the circle.

If the angle between two radii of a circle is 130°, then the angle between the tangents at the ends of the radii is ______
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
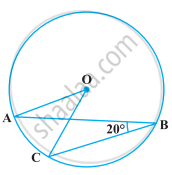
In the following figure, if ∠ABC = 20º, then ∠AOC is equal to ______.