Advertisements
Advertisements
प्रश्न
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
उत्तर
Given ΔABC is isosceles AB = AC
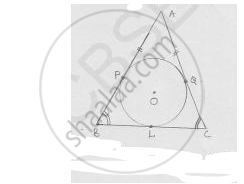
We know that
The tangents from external point to circle are equal in length
From point A, AP = AQ
But AB = AC ⇒ AP + PB = AQ + QC
⇒ PB = PC …. (i)
From B, PB = BL; ….(ii) from C, CL = CQ …..(iii)
From (i), (ii) & (iii)
BL = CL
∴ L bisects BC.
APPEARS IN
संबंधित प्रश्न
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
From an external point P , tangents PA = PB are drawn to a circle with centre O . If \[\angle PAB = {50}^o\] , then find \[\angle AOB\]
In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

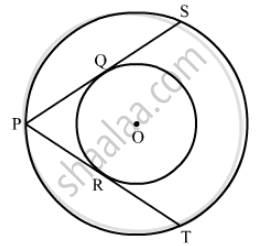
In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
The point of concurrence of all angle bisectors of a triangle is called the ______.
Construct a triangle XYZ in which XY = YZ= 4.5 cm and ZX = 5.4 cm. Draw the circumcircle of the triangle and measure its circumradius.
Find the diameter of the circle
Radius = 6 cm
Given: A circle inscribed in a right angled ΔABC. If ∠ACB = 90° and the radius of the circle is r.
To prove: 2r = a + b – c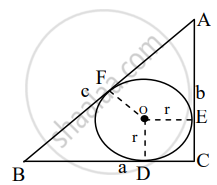
If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°.
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
