Advertisements
Advertisements
प्रश्न
In the given figure, PO

उत्तर
In the given figure,
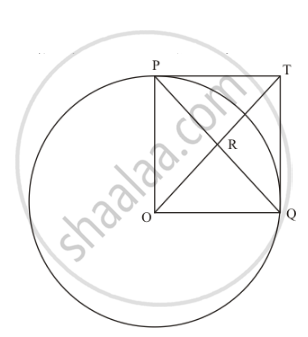
PO = OQ (Since they are the radii of the same circle)
PT = TQ (Length of the tangents from an external point to the circle will be equal) Now considering the angles of the quadrilateral PTQO, we have,
We know that the sum of all angles of a quadrilateral will be equal to
Thus we have found that all angles of the quadrilateral are equal to 90°.
Since all angles of the quadrilateral PTQO are equal to 90° and the adjacent sides are equal, this quadrilateral is a square.
We know that in a square, the diagonals will bisect each other at right angles.
Therefore, PQ and OT bisect each other at right angles.
Thus we have proved.
APPEARS IN
संबंधित प्रश्न
Prove that in two concentric circles, the chord of the larger circle which touches the smaller circle, is bisected at the point of contact.
Fill in the blanks:
The centre of a circle lies in ____________ of the circle.
true or false
The degree measure of an arc is the complement of the central angle containing the arc.
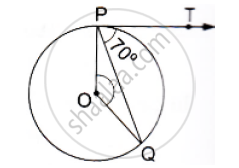
If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.
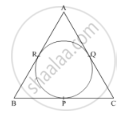
In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
In Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of the side AD.
Draw two circles of different radii. How many points these circles can have in common? What is the maximum number of common points?
Suppose you are given a circle. Describe a method by which you can find the center of this circle.
Two concentric circles with center O have A, B, C, D as the points of intersection with the lines L shown in the figure. If AD = 12 cm and BC s = 8 cm, find the lengths of AB, CD, AC and BD.
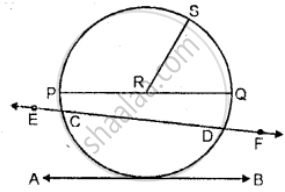
Use the figure given below to fill in the blank:
________ is a radius of the circle.