Advertisements
Advertisements
प्रश्न
Suppose you are given a circle. Describe a method by which you can find the center of this circle.
उत्तर
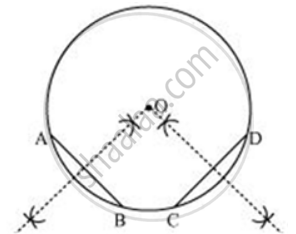
To draw the center of a given circle :
1. Draw the circle.
2. Take any two different chords AB and CD of this circle and draw perpendicular bisector of these chords.
3. let these perpendicular bisectors meet at point O.
So, O will be the center of the given circle.
APPEARS IN
संबंधित प्रश्न
Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y). Find the values of y. Hence find the radius of the circle.
Write True or False. Give reasons for your answers.
A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
If AB, AC, PQ are tangents in Fig. and AB = 5cm find the perimeter of ΔAPQ.
In figure OQ : PQ = 3 : 4 and perimeter of ΔPDQ = 60cm. determine PQ, QR and OP.
The greatest chord of a circle is called its
Draw two circles of different radii. How many points these circles can have in common? What is the maximum number of common points?
A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
In the adjoining figure, seg DE is the chord of the circle with center C. seg CF⊥ seg DE and DE = 16 cm, then find the length of DF?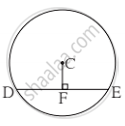
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
From the figure, identify a sector.

