Advertisements
Advertisements
प्रश्न
A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
विकल्प
25 cm
20 cm
40 cm
18 cm
उत्तर
40 cm
Explanation;
Hint: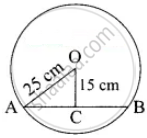
In the right triangle OAC,
AC2 = OA2 – OC2
= 252 – 152
= (25 + 15)(25 – 15)
= 40 × 10
AC2 = 400
AC = `sqrt(400)`
= 20
Length of the chord AB = 20 + 20 = 40 cm.
APPEARS IN
संबंधित प्रश्न
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
In the below fig. O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

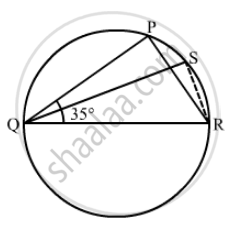
In the given figure, ΔPQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.
Construct a triangle ABC with AB = 5 cm, ∠B = 60° and BC = 6. 4 cm. Draw the incircle of the triangle ABC.
AD is a diameter of a circle and AB is a chord If AD = 30 cm and AB = 24 cm then the distance of AB from the centre of the circle is
The radius of a circle of diameter 24 cm is _______
A part of circumference of a circle is called as _______
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.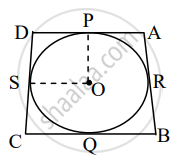
AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.
From the figure, identify a sector.

