Advertisements
Advertisements
प्रश्न
AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.
उत्तर

Given: We have a circle whose centre is O and chords AB and AC are equal. AM is the bisector of ∠BAC.
To prove: Centre O lies on the bisector of ∠BAC.
Construction: Join BM and CM.
Proof: In ΔBAM and ΔCAM,
AB = AC ...[Given]
∠BAM = ∠CAM ...[Given]
AM = AM ...[Common]
∴ ΔBAM ≅ ΔCAM ...[By SAS congruency]
`\implies` BM = CM [By C.P.C.T.] ...(i)
And ∠BMA = ∠CMA [By C.P.C.T.] ...(ii)
In ΔBOM and ΔCOM,
BM = CM ...[By (i)]
OM = OM ...[Common]
∠BMO = ∠CMO ...[By (ii)]
∴ ΔBOM and ΔCOM ...[By SAS congruency]
`\implies` ∠BOM = ∠COM [By C.P.C.T.] ...(iii)
Since, ∠BOM + ∠COM = 180° ...(iv)
∴ By (iii) and (iv), ∠BOM = ∠COM = 90°
So, AM is the perpendicular bisector of the chord BC.
Thus, bisector of ∠BAC i.e., AM passes through the centre O.
APPEARS IN
संबंधित प्रश्न
From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of line segment PQ.
Find the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
From an external point P, tangents PA and PB are drawn to the circle with centre O. If CD is the tangent to the circle at point E and PA = 14 cm. Find the perimeter of ABCD.
In fig. there are two concentric circles with Centre O of radii 5cm and 3cm. From an
external point P, tangents PA and PB are drawn to these circles if AP = 12cm, find the
tangent length of BP.
Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
In following fig. ABC is an equilateral triangle . A circle is drawn with centre A so that ot cuts AB and AC at M and N respectively. Prove that BN = CM.

Draw circle with the radii given below.
2 cm
In the table below, write the names of the points in the interior and exterior of the circle and those on the circle.
| Diagram | Points in the interior of the circle |
Points in the exterior of the circle |
Points on the circle |
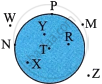 |
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 1760 cm |
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
