Advertisements
Advertisements
प्रश्न
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 1760 cm |
उत्तर
Given: Circumference C = 1760 cm
2πr = 1760
`2 xx 22/7 xx "r"` = 1760
r = `(1760 xx 7)/(2 xx 22)`
= `(160 xx 7)/(2 xx 2)`
= 40 × 7
= 280 cm
diameter = 2 × r
= 2 × 280
= 560 cm
Tabulating the results
| radius (r) | diameter (d) | Circumference (C) |
| 280 cm | 560 cm | 1760 cm |
APPEARS IN
संबंधित प्रश्न
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

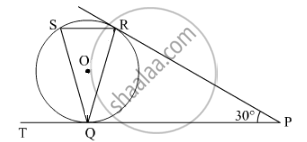
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
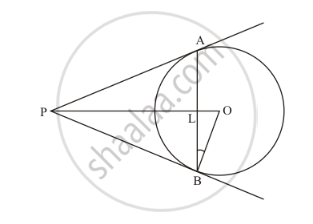
PA and PB are tangents from P to the circle with centre O. At point M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
If the tangent at point P to the circle with center O cuts a line through O at Q such that PQ= 24cm and OQ = 25 cm. Find the radius of circle
In the given figure, AB is a chord of length 16 cm of a circle of radius 10 cm. The tangents at A and B intersect at a point P. Find the length of PA.
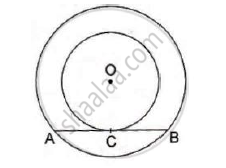
In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.
A circle is inscribed in a ΔABC touching AB, BC and AC at P, Q and R respectively. If AB = 10 cm, AR=7cm and CR=5cm, find the length of BC.

In two concentric circles, a chord of length 8 cm of the large circle touches the smaller circle. If the radius of the larger circle is 5 cm, then find the radius of the smaller circle.
In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
Use the figure given below to fill in the blank:
Diameter of a circle is ______.

Construct a triangle ABC with AB = 4.2 cm, BC = 6 cm and AC = 5cm. Construct the circumcircle of the triangle drawn.
Draw circle with the radii given below.
3 cm
Draw circle with the radii given below.
4 cm
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
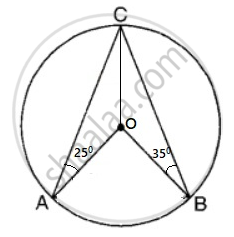
In the adjoining figure ‘O’ is the center of the circle, ∠CAO = 25° and ∠CBO = 35°. What is the value of ∠AOB?
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.
