Advertisements
Advertisements
प्रश्न
In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
उत्तर
It is given that
ABCD is cyclic quadrilateral and ` m angle A = 3 (m angle C ) `
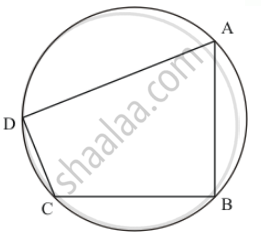
We have to find `m angle A `
Since ABCD is cyclic quadrilateral and sum of opposite pair of cyclic quadrilateral is 180°.
So ` angle A + angle C = 180°`
And
`3angleC + angleC = 180°`
`4angleC = 180°`
`angleC = (180°)/4`
= 45°
Therefore
`angleA = 3 xx 45° `
= 135°
Hence `angle A = 135°`
APPEARS IN
संबंधित प्रश्न
In Fig. 1, QR is a common tangent to the given circles, touching externally at the point T. The tangent at T meets QR at P. If PT = 3.8 cm, then the length of QR (in cm) is :
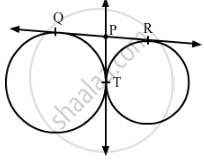
(A) 3.8
(B) 7.6
(C) 5.7
(D) 1.9
In two concentric circles, prove that all chords of the outer circle which touch the inner circle are of equal length.
From an external point P , tangents PA = PB are drawn to a circle with centre O . If \[\angle PAB = {50}^o\] , then find \[\angle AOB\]
The length of three concesutive sides of a quadrilateral circumscribing a circle are 4 cm, 5 cm, and 7 cm respectively. Determine the length of the fourth side.
Find the radius of the circle
Diameter = 76 cm
In the adjoining figure, seg DE is the chord of the circle with center C. seg CF⊥ seg DE and DE = 16 cm, then find the length of DF?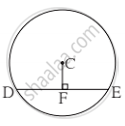
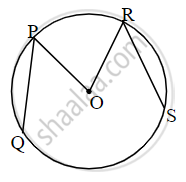
In figure, O is the centre of a circle, chord PQ ≅ chord RS. If ∠POR = 70° and (arc RS) = 80°, find
(i) m(arc PR)
(ii) m(arc QS)
(iii) m(arc QSR)
A point A is 26 cm away from the centre of a circle and the length of the tangent drawn from A to the circle is 24 cm. Find the radius of the circle.
If an isosceles triangle ABC, in which AB = AC = 6 cm, is inscribed in a circle of radius 9 cm, find the area of the triangle.
AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.
