Advertisements
Advertisements
प्रश्न
The length of three concesutive sides of a quadrilateral circumscribing a circle are 4 cm, 5 cm, and 7 cm respectively. Determine the length of the fourth side.
उत्तर
Let us first put the given data in the form of a diagram.
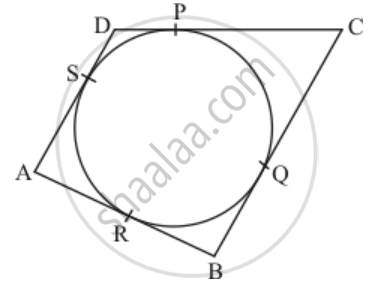
From the property of tangents we know that the length of two tangents drawn from the same external point will be equal. Therefore we have,
AR = SA
Let us represent AR and SA by ‘a’.
Similarly,
QB = RB
Let us represent SD and DP by ‘b’
PC = CQ
Let us represent PC and PQ by ‘c’
SD = DP
Let us represent QB and RB by ‘d’
It is given that,
AB = 4
AR + RB =4
a + b = 4
b = 4 − a …… (1)
Similarly,
BC = 5
That is,
b + c = 5
Let us substitute for b from equation (1). We get,
4 − a + c = 5
c − a = 1
c = a + 1 …… (2)
CD = 7
c + d = 7
Let us substitute for c from equation (2). We get,
a + 1 + d = 7
a + d = 6
In the previous section we had represented AS and SR with ‘a’ and SD and DP with ‘b’. We shall now put AS in place of ‘a’ and SD in place of ‘d’. We get,
AS + SD = 6
AD = 6 cm
Therefore, the length of the fourth side of the quadrilateral is 6 cm.
APPEARS IN
संबंधित प्रश्न
From a point P, two tangents PA and PB are drawn to a circle with center O. If OP =
diameter of the circle shows that ΔAPB is equilateral.
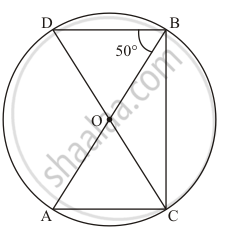
In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
The circle which passes through all the vertices of a triangle is called ______.
Draw circle with the radii given below.
4 cm
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, find ∠CBA see figure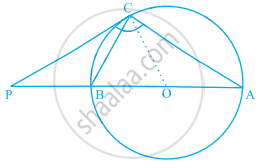
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
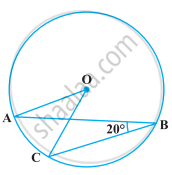
In the following figure, if ∠ABC = 20º, then ∠AOC is equal to ______.
On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.
The circumcentre of the triangle ABC is O. Prove that ∠OBC + ∠BAC = 90º.
From the figure, identify two points in the interior.

