Advertisements
Advertisements
प्रश्न
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, find ∠CBA see figure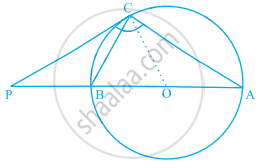
उत्तर
Here, AB is a diameter of the circle from point C and a tangent is drawn which meets at a point P.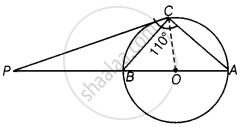
Join OC.
Here, OC is radius.
Since, tangent at any point of a circle is perpendicular to the radius through point of contact circle.
∴ OC ⊥ PC
Now, ∠PCA = 110° ...[Given]
⇒ ∠PCO + ∠OCA = 110°
⇒ 90° + ∠OCA = 110°
⇒ ∠OCA = 20°
∴ OC = OA = Radius of circle
⇒ ∠OCA = ∠OAC = 20° ...[Since, two sides are equal, then their opposite angles are equal]
Since, PC is a tangent,
So ∠BCP = ∠CAB = 20° ...[Angles in a alternate segment are equal]
In ΔPBC,
∠P + ∠C + ∠A = 180°
∠P = 180° – (∠C + ∠A)
= 180° – (110° + 20°)
= 180° – 130°
= 50°
In ΔPBC,
∠BPC + ∠PCB + ∠PBC = 180° ...[Sum of all interior angles of any triangle is 180°]
⇒ 50° + 20° + ∠PBC = 180°
⇒ ∠PBC = 180° – 70°
⇒ ∠PBC = 110°
Since, APB is a straight line.
∴ ∠PBC + ∠CBA = 180°
⇒ ∠CBA = 180° – 110° = 70°
संबंधित प्रश्न
Fill in the blanks:
The longest chord of a circle is a __________ of the circle.
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
In fig. a circle touches all the four sides of quadrilateral ABCD with AB = 6cm, BC = 7cm, CD = 4cm. Find AD.
In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.

In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

Can the length of a chord of a circle be greater than its diameter ? Explain.
State, if the following statement is true or false:
Every diameter bisects a circle and each part of the circle so obtained is a semi-circle.
Draw circle with the radii given below.
3 cm
If the radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is ______
From the figure, identify a point in the exterior.

