Advertisements
Advertisements
प्रश्न
In figure, O is the centre of a circle of radius 5 cm, T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.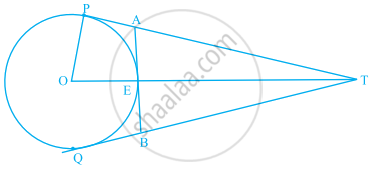
उत्तर
Given: A circle with center O and radius = 5 cm T is a point, OT = 13 cm. OT intersects the circle at E and AB is the tangent to the circle at E.
To Find: Length of AB
OP ⊥ PT ...[Tangent at a point on the circle is perpendicular to the radius through point of contact]
By pythagoras theorem in ∆OPT right angled at P
(OT)2 = (OP)2 + (PT)2
(13)2 = (5)2 + (PT)2
(PT)2 = 169 – 25 = 144
PT = 12 cm
PT = TQ = 12 cm ...[Tangents drawn from an external point to a circle are equal]
Now, OT = OE + ET
ET = OT – OE
= 13 – 5
= 8 cm
Now, as Tangents drawn from an external point to a circle are equal.
AE = PA ...[1]
EB = BQ ...[2]
Also OE ⊥ AB ...[Tangent at a point on the circle is perpendicular to the radius through point of contact]
∠AEO = 90°
∠AEO + ∠AET = 180° ...[By linear Pair]
∠AET = 90°
In ΔAET By Pythagoras Theorem
(AT)2 = (AE)2 + (ET)2 ...[Here AE = PA as tangents drawn from an external point to a circle are equal]
(PT – PA)2 = (PA)2 + (ET)2
(12 – PA)2 = (PA)2 + (8)2 ...[From 1]
144 + (PA)2 – 24PA = (PA)2 + 64
24PA = 80 ...[3]
∠AET + ∠BET = 180° ...[Linear Pair]
90° + ∠BET = 180°
∠BET = 90°
In ΔBET, By Pythagoras Theorem
(BT)2 = (BE)2 + (ET)2
(TQ – BQ)2 = (BQ)2 + (ET)2 ...[From 2]
(12 – BQ)2 = (BQ)2 + (8)2
144 + (BQ)2 – 24BQ = (BQ)2 + 64
24BQ = 80 ...[4]
So, AB = AE + BE
AB = PA + BQ ...[From 1 and 2]
AB = `10/3 + 10/3` ...[From 3 and 4]
AB = `20/3` cm
APPEARS IN
संबंधित प्रश्न
From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
If Δ ABC is isosceles with AB = AC and C (O, r) is the incircle of the ΔABC touching BC at L,prove that L bisects BC.
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
The length of the direct common tangent to two circles of radii 12cm and 4cm is 15cm. calculate the distance between their centres.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate ∠ PAD.

In the following figure, seg AB is the diameter of the circle with center P. Line CB be the tangent and line AC intersects a circle in point D. Prove that:
AC x AD = 4 (radius)2

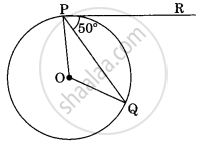
In figure, if O is the centre of a circle PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to ______.
Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
In the given figure, PA is a tangent to the circle drawn from the external point P and PBC is the secant to the circle with BC as diameter. If ∠AOC = 130°, then find the measure of ∠APB, where O is the centre of the circle.

