Advertisements
Advertisements
प्रश्न
From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
विकल्प
A. 25
B. `sqrt313`
C. 5
D. 1
उत्तर
The given information can be represented diagrammatically as follows:

Let O be the centre of the circle.
Given: PQ = 12 cm and OQ = 13 cm.
To find: Radius of the circle
PQ is a tangent drawn from the external point Q to the circle.
∠ OPQ = 90° (Radius is perpendicular to the tangent at the point of contact)
On applying Pythagoras theorem in ΔOPQ, we obtain:
OQ2 = OP2 + PQ2
∴ OP2 = OQ2 − PQ2
⇒ OP2 = (13 cm)2 − (12 cm)2
⇒ OP2 = 169cm2 − 144 cm2
⇒ OP2 = 25 cm2
⇒ OP = 5 cm
Thus, the radius of circle is 5 cm.
Hence, the correct answer is C
APPEARS IN
संबंधित प्रश्न
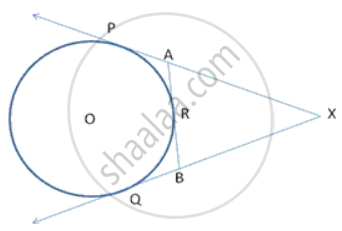
In the figure, XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that XA + AR = XB + BR.
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle AOB

In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle APB

In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)

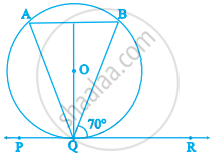
In figure, if PQR is the tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to ______.
The tangents drawn at the extremities of the diameter of a circle are ______.
In Question 5 above, if radii of the two circles are equal, prove that AB = CD.
In figure, O is the centre of a circle of radius 5 cm, T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.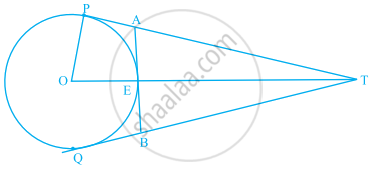
In the given figure, AB is diameter of a circle centered at O. BC is tangent to the circle at B. If OP bisects the chord AD and ∠AOP = 60°, then find ∠C.
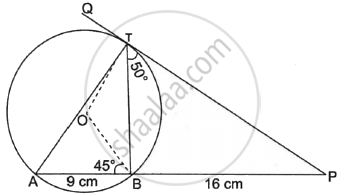
In the given figure, O is the centre of the circle. PQ is a tangent to the circle at T. Chord AB produced meets the tangent at P.
AB = 9 cm, BP = 16 cm, ∠PTB = 50° ∠OBA = 45°
Find:
- Length of PT
- ∠BAT
- ∠BOT
- ∠ABT