Advertisements
Advertisements
प्रश्न
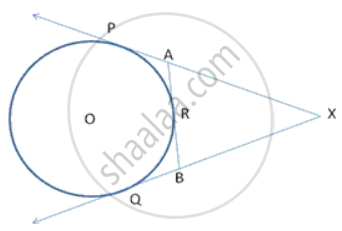
In the figure, XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that XA + AR = XB + BR.
उत्तर
XP = XQ
AR = AP
BR = BQ {Length of tangents drawn from an external point to a circle are equal}
XP = XQ
XA + AP = XB + BR
XA + AR = XB + BR {Using {1)}
APPEARS IN
संबंधित प्रश्न
A circle can have ______ parallel tangents at the most.
The common point of a tangent to a circle and the circle is called ______.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is ______.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

In the given Figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°. Then ∠BOC is equal to ______
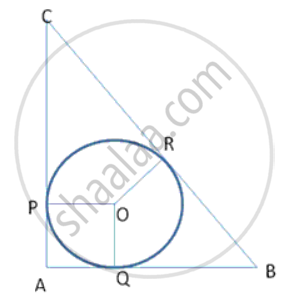
In following fig., ABC is a right- angled triangle at A with sides AB = 5 cm and BC = 13 cm . A circle with centre O has been inscribed in the triangle ABC. Calculate the radius of the incircle.
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ALOB is a cyclic quadrilateral.
Two circle with radii r1 and r2 touch each other externally. Let r be the radius of a circle which touches these two circle as well as a common tangent to the two circles, Prove that: `1/sqrtr + 1/sqrtr_1 + 1/sqrtr_2`.
In figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to ______.

Find the value of ∠DCE.

