Advertisements
Advertisements
प्रश्न
Two circle with radii r1 and r2 touch each other externally. Let r be the radius of a circle which touches these two circle as well as a common tangent to the two circles, Prove that: `1/sqrtr + 1/sqrtr_1 + 1/sqrtr_2`.
उत्तर
From the adjoining figure,
PQ = SY = `sqrt( "XY"^2 - "XS"^2)`
= `sqrt((r_1 + r_2)^2 - (r_1 - r_2)^2)`
= `sqrt(4r_1r_2)`
= `sqrt(r_1r_2)`
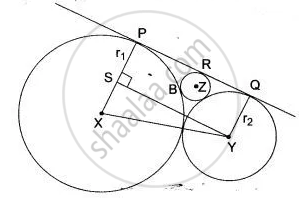
Similarly, PR = `2 sqrt(rr_1)` and RQ = `2 sqrt(rr_2)`
Now, PQ = PR + RQ
`2 sqrt(r_1r_2) = 2 sqrt(rr_1) = 2 sqrt(rr_2) `
⇒ `sqrt(r_1r_2) = sqrt(rr_1) = sqrt(rr_2) `
Dividing by `sqrt(rr_1r_2)` on both sides,
⇒ `1/sqrtr + 1/sqrtr_1 + 1/sqrtr_2`.
Hence proved.
APPEARS IN
संबंधित प्रश्न
How many tangents can a circle have?
A circle can have ______ parallel tangents at the most.
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.

How many common tangents can be drawn to two circles, touching each
other externally?
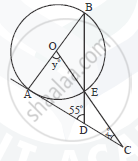
In the given figure AC is a tangent to the circle with centre O.
If ∠ADB = 55° , find x and y. Give reasons for your answers.
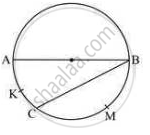
In the following figure, seg AB is a diameter of the circle, m (arc AKC) = 40°. Find the value of m (arc BMC).
Draw a circle of radius 2.7 cm and draw a chord PQ of length 4.5 cm. Draw tangents at points P and Q without using centre.
In figure, M is the centre of the circle and seg KL is a tangent segment. If MK = 12, KL = `6sqrt(3)`, then find
(i) Radius of the circle.
(ii) Measures of ∠K and ∠M.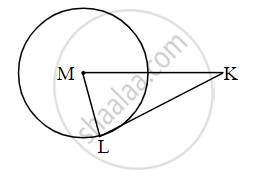
In the given figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 25°, then x is equal to ______.

