Advertisements
Advertisements
Question
Two circle with radii r1 and r2 touch each other externally. Let r be the radius of a circle which touches these two circle as well as a common tangent to the two circles, Prove that:
Solution
From the adjoining figure,
PQ = SY =
=
=
=
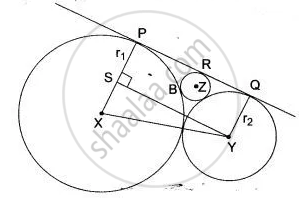
Similarly, PR =
Now, PQ = PR + RQ
⇒
Dividing by
⇒
Hence proved.
APPEARS IN
RELATED QUESTIONS
In the figure given below, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ.

In the given figure O is the centre of the circle. Tangents A and B meet at C. If ∠ACO = 30°, find
1) ∠BCO
2) ∠AOB
3) ∠APB
What is the distance between two parallel tangents of a circle having radius 4.5 cm ? Justify your answer.
Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (ii) radius of the circle.

In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find AB.

ABC is a right triangle with angle B = 90º. A circle with BC as diameter meets by hypotenuse AC at point D. Prove that: BD2 = AD × DC.
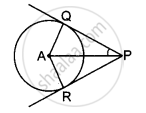
In the figure, PQ and PR are tangents to a circle with centre A. If ∠QPA=27°, then ∠QAR equals to ______
A tangent JK is drawn to a circle with centre C such that CK = 6 cm and ∠CKJ = 60°. Find the length of the tangent JK.

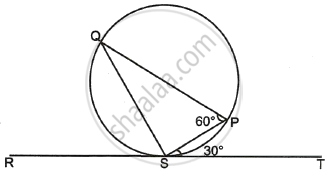
In the given diagram RT is a tangent touching the circle at S. If ∠PST = 30° and ∠SPQ = 60°, then ∠PSQ is equal to ______.