Advertisements
Advertisements
Question
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find AB.

Solution
PA = AB + BP = (AB + 4) cm
PC = PD + CD = 5 + 7.8 = 12.8 cm
Since PA × PB = PC × PD
⇒ (AB + 4) × 4 = 12.8 × 5
⇒ AB + 4 =
⇒ AB + 4 = 16
⇒ AB = 12 cm
APPEARS IN
RELATED QUESTIONS
A tangent to a circle intersects it in ______ point (s).
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

In the following figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
What is the distance between two parallel tangents of a circle having radius 4.5 cm ? Justify your answer.
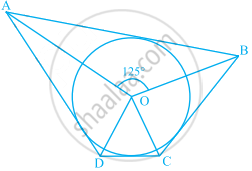
In figure, if ∠AOB = 125°, then ∠COD is equal to ______.
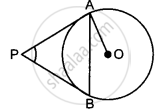
In the figure PA and PB are tangents to the circle with centre O. If ∠APB = 60°, then ∠OAB is ______
Construct a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
A circle of radius 5.2 cm has two tangents AB and CD parallel to each other. What is the distance between the two tangents?
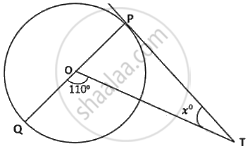
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.