Advertisements
Advertisements
Question
What is the distance between two parallel tangents of a circle having radius 4.5 cm ? Justify your answer.
Solution 1
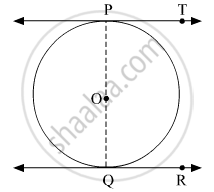
In the given figure, O is the centre of the circle. Line PT and line QR are two parallel tangents to the circle at P and Q, respectively.
∴ ∠OPT + ∠OQR = 180º ......(Sum of adjacent interior angles on the same side of the transversal is supplementary)
⇒ POQ is a straight line segment.
∴ PQ is the diameter of the circle.
PQ = Distance between the parallel tangents PT and QR
= 2 × Radius
= 2 × 4.5
= 9 cm
Thus, the distance between two parallel tangents of the circle is 9 cm.
Solution 2
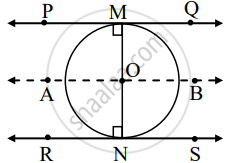
Let the lines PQ and RS be the two parallel tangents to circle at M and N respectively.
Through centre O, draw line AB || line RS.
OM = ON = 4.5 ......[Given]
Line AB || line RS ......[Construction]
Line PQ || line RS ......[Given]
∴ Line AB || line PQ || line RS
Now, ∠OMP = ∠ONR = 90° ......(i) [Tangent theorem]
For line PQ || line AB,
∠OMP = ∠AON = 90° ......(ii) [Corresponding angles and from (i)]
For line RS || line AB,
∠ONR = ∠AOM = 90° (iii) ......Corresponding angles and from (i)]
∠AON + ∠AOM = 90° + 90° ......[From (ii) and (iii)]
∴ ∠AON + ∠AOM = 180°
∴ ∠AON and ∠AOM form a linear pair.
∴ Ray OM and ray ON are opposite rays.
∴ Points M, O, N are collinear. ......(iv)
∴ MN = OM + ON ......[M−O–N, From (iv)]
∴ MN = 4.5 + 4.5
∴ MN = 9 cm
∴ Distance between two parallel tangents PQ and RS is 9 cm.
APPEARS IN
RELATED QUESTIONS
The common point of a tangent to a circle and the circle is called ______.
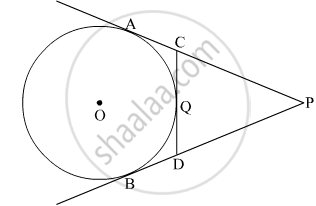
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
Find the length of the tangent from a point which is at a distance of 5cm from the centre of the circle of radius 3cm.
In followinf fig., two concentric circles with centre 0 are of radii 5 cm and 3 cm. from an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.
In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)

In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
- AB.
- the length of tangent PT.
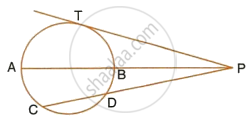
At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is ______
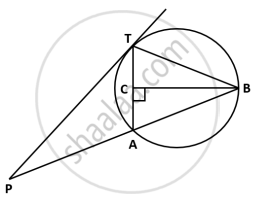
In the given figure, PT is a tangent to the circle at T, chord BA is produced to meet the tangent at P. Perpendicular BC bisects the chord TA at C. If PA = 9 cm and TB = 7 cm, find the lengths of:
- AB
- PT
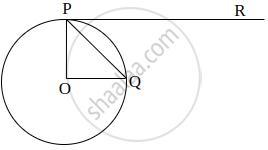
How many tangents can be drawn to a circle from a point on it?
In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.

If O is centre of a circle and Chord PQ makes an angle 50° with the tangent PR at the point of contact P, then the angle subtended by the chord at the centre is ______.
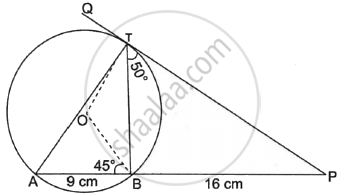
In the given figure, O is the centre of the circle. PQ is a tangent to the circle at T. Chord AB produced meets the tangent at P.
AB = 9 cm, BP = 16 cm, ∠PTB = 50° ∠OBA = 45°
Find:
- Length of PT
- ∠BAT
- ∠BOT
- ∠ABT
In the given diagram an isosceles ΔABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°.

Find:
- ∠ABC
- ∠BAC
- ∠BCQ
