Advertisements
Advertisements
प्रश्न
What is the distance between two parallel tangents of a circle having radius 4.5 cm ? Justify your answer.
उत्तर १
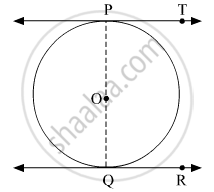
In the given figure, O is the centre of the circle. Line PT and line QR are two parallel tangents to the circle at P and Q, respectively.
∴ ∠OPT + ∠OQR = 180º ......(Sum of adjacent interior angles on the same side of the transversal is supplementary)
⇒ POQ is a straight line segment.
∴ PQ is the diameter of the circle.
PQ = Distance between the parallel tangents PT and QR
= 2 × Radius
= 2 × 4.5
= 9 cm
Thus, the distance between two parallel tangents of the circle is 9 cm.
उत्तर २
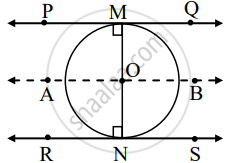
Let the lines PQ and RS be the two parallel tangents to circle at M and N respectively.
Through centre O, draw line AB || line RS.
OM = ON = 4.5 ......[Given]
Line AB || line RS ......[Construction]
Line PQ || line RS ......[Given]
∴ Line AB || line PQ || line RS
Now, ∠OMP = ∠ONR = 90° ......(i) [Tangent theorem]
For line PQ || line AB,
∠OMP = ∠AON = 90° ......(ii) [Corresponding angles and from (i)]
For line RS || line AB,
∠ONR = ∠AOM = 90° (iii) ......Corresponding angles and from (i)]
∠AON + ∠AOM = 90° + 90° ......[From (ii) and (iii)]
∴ ∠AON + ∠AOM = 180°
∴ ∠AON and ∠AOM form a linear pair.
∴ Ray OM and ray ON are opposite rays.
∴ Points M, O, N are collinear. ......(iv)
∴ MN = OM + ON ......[M−O–N, From (iv)]
∴ MN = 4.5 + 4.5
∴ MN = 9 cm
∴ Distance between two parallel tangents PQ and RS is 9 cm.
APPEARS IN
संबंधित प्रश्न
A line intersecting a circle in two points is called a ______.
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
In the given figure O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of a circle.

In the given figure, find TP if AT = 16 cm and AB = 12 cm.

In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.

Four alternative answers for the following question is given. Choose the correct alternative.
If two circles are touching externally, how many common tangents of them can be drawn?
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
Two chords AB and CD of lengths 6cm and 12cm are drawn parallel inside the circle. If the distance between the chords of the circle is 3cm, find the radius of the circle.
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
A point A is 17cm from the centre of the circle. The length of the tangent drawn from A to the circle is 15cm. find the radius of the circle.
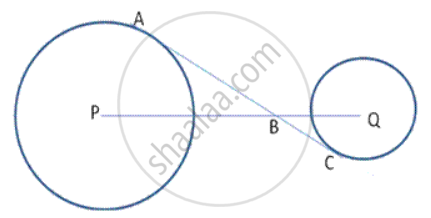
In the following fig. , AC is a transversal common tangent to tvvo circles with centres P and Q and of radii 6cm and 3cm respectively. Given that AB = 8cm, calculate PQ.
PA and PB are tangents from P to the circle with centre O. At M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ALOB is a cyclic quadrilateral.
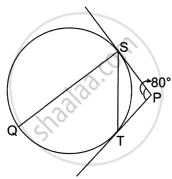
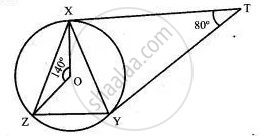
In the alongside, figure, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°. Calculate the value of ∠ZXY.
The tangents drawn at the extremities of the diameter of a circle are ______.
How many tangents can be drawn to a circle from a point on it?
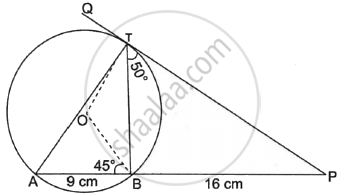
In the given figure, O is the centre of the circle. PQ is a tangent to the circle at T. Chord AB produced meets the tangent at P.
AB = 9 cm, BP = 16 cm, ∠PTB = 50° ∠OBA = 45°
Find:
- Length of PT
- ∠BAT
- ∠BOT
- ∠ABT
In the given figure O, is the centre of the circle. CE is a tangent to the circle at A. If ∠ABD = 26° find:
- ∠BDA
- ∠BAD
- ∠CAD
- ∠ODB

In the given diagram, PS and PT are the tangents to the circle. SQ || PT and ∠SPT = 80°. The value of ∠QST is ______.