Advertisements
Advertisements
प्रश्न
In the given figure O, is the centre of the circle. CE is a tangent to the circle at A. If ∠ABD = 26° find:
- ∠BDA
- ∠BAD
- ∠CAD
- ∠ODB

उत्तर
Given ∠ABD = 26°
a. Angle in semi-circle is a right angle
∴ ∠BDA = 90°

b. Sum of all angles in a triangle = 180°
∴ ∠BAD + ∠BDA + ∠ABD = 180°
∠BAD + 90° + 26° = 180°
∠BAD = 180° – 116°
= 64°
c. Angles in alternate segments are equal
∴ ∠CAD = ∠ABD
= 26°
d. In ΔODB,
OB = OD ...(Radii of same circle)
∴ ∠ODB = ∠OBD
= ∠ABD
= 26°
APPEARS IN
संबंधित प्रश्न
In Fig. 1, PQ is a tangent at a point C to a circle with centre O. if AB is a diameter and ∠CAB = 30°, find ∠PCA.

A circle can have ______ parallel tangents at the most.
In the given figure O is the centre of the circle. Tangents A and B meet at C. If ∠ACO = 30°, find
1) ∠BCO
2) ∠AOB
3) ∠APB
In the following figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
The given figure shows a circle with centre O and BCD is tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.

In Figure 3, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths of 8 cm and 6 cm respectively, find the value of r.

Four alternative answers for the following question is given. Choose the correct alternative.
If two circles are touching externally, how many common tangents of them can be drawn?
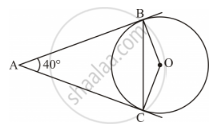
In the given Figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°. Then ∠BOC is equal to ______
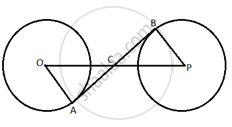
The distance between the centres of equal circles each of radius 3 cm is 10 cm. The length of a transverse tangent AB is ______

In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
