Advertisements
Advertisements
प्रश्न

In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
उत्तर
Proof: From figure

Seg AB ⊥ seg BC and seg AD ⊥ seg CD .......[By tangent theorem]
∴ ∠ABC = ∠ADC = 90°
In □ABCD,
∠A + ∠B + ∠C + ∠D = 360° ......[Angle of the square]
∴ ∠A + 90° + ∠C + 90° = 360°
∴ ∠A + ∠C = 360° – 180°
∴ ∠A + ∠C = 180°
∴ ∠A + m(arc BXD) = 180° [Central angle] ......(i)
Now, m(arc BXD) + m(arc BYD) = 360° ......[Two arcs contribute a complete circle] ......(ii)
Now, multiply equation (i) by 2 on both sides
2[∠A + m(arc BXD)] = 2 × 180°
∴ 2∠A + 2 × m(arc BXD) = 360°
∴ 2∠A = 360 – 2 × m(arc BXD)
∴ 2∠A = m(arc BXD) + m(arc BYD) – 2m(arc BXD)
∴ 2∠A = m(arc BYD) – m(arc BXD) .....[From (ii)]
∴ ∠A = `1/2` [m(arc BYD) – m(arc BXD)]
Hence proved.
APPEARS IN
संबंधित प्रश्न
In Fig. 1, PQ is a tangent at a point C to a circle with centre O. if AB is a diameter and ∠CAB = 30°, find ∠PCA.

A line intersecting a circle in two points is called a ______.
If the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is 60°, then find the length of OP
In the given figure, find TP if AT = 16 cm and AB = 12 cm.

In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.

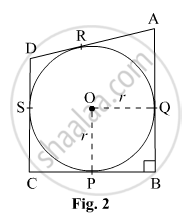
In Fig.2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm, then the radius of the circle (in cm.) is:
From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
In Figure 1, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC
= 4 cm, then the length of AP (in cm) is
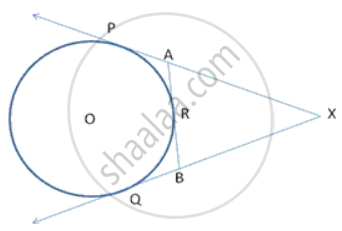
In the figure, XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that XA + AR = XB + BR.
ABC is a right triangle with angle B = 90º. A circle with BC as diameter meets by hypotenuse AC at point D. Prove that: BD2 = AD × DC.
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ALOB is a cyclic quadrilateral.
In the following figure, seg AB is the diameter of the circle with center P. Line CB be the tangent and line AC intersects a circle in point D. Prove that:
AC x AD = 4 (radius)2

If PA and PB are two tangents drawn from a point P to a circle with center C touching it A and B, prove that CP is the perpendicular bisector of AB.
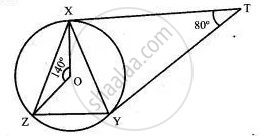
In the alongside, figure, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°. Calculate the value of ∠ZXY.
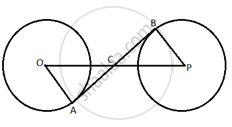
Two parallel lines touch the circle at
points A and B respectively. If the area of the circle is 25 n cm2, then AB is equal to ______
The distance between the centres of equal circles each of radius 3 cm is 10 cm. The length of a transverse tangent AB is ______
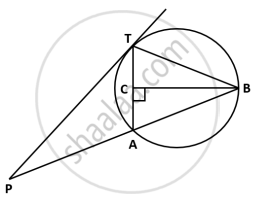
In the given figure, PT is a tangent to the circle at T, chord BA is produced to meet the tangent at P. Perpendicular BC bisects the chord TA at C. If PA = 9 cm and TB = 7 cm, find the lengths of:
- AB
- PT
Construct a pair of tangents to a circle of radius 4 cm, which are inclined to each other at an angle of 60°.
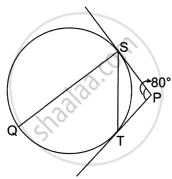
In the given diagram, PS and PT are the tangents to the circle. SQ || PT and ∠SPT = 80°. The value of ∠QST is ______.
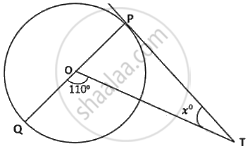
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.