Advertisements
Advertisements
प्रश्न
Find the co-ordinates of centroid of a triangle if points D(–7, 6), E(8, 5) and F(2, –2) are the mid-points of the sides of that triangle.
उत्तर
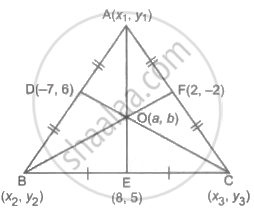
Let A(x1, y1), B(x2, y2) and C(x3, y3) be the vertices of MBC.
Given that D(–7, 6), E(8, 5) and F(2, –2) are the midpoints of sides AB, BC and AC respectively.
Let G(x, y) be the centroid.
D is now the midpoint of AB.
∴ By midpoint formula.
–7 = `(x_1 + x_2)/2`
∴ x1 + x2 = –7 × 2
∴ x1 + x2 = –14 ......(i)
Similarly x2 + x3 = 16 ......(ii)
And x1 + x3 = 4 ......(iii)
Adding equations (i), (ii), and (iii), we get
x1 + x2 + x2 + x3 + x1 + x3 = –14 + 16 + 4
∴ 3x1 + 2x2 + 2x3 = 6
∴ 2(x1 + x2 + x3) = 6
∴ x1 + x2 + x3 = `6/2`
∴ x1 + x2 + x3 = 3 ......(iv)
D is the midpoint of AB.
∴ By the midpoint formula,
6 = `("y"_1 + "y"_2)/2`
∴ y1 + y2 = 12 ......(v)
Similarly, y2 + y3 = 10 ......(vi)
y1 + y3 = –4 ......(vii)
Adding equations (v), (vi), and (vii), we get
y1 + y2 + y2 + y3 + y1 + y4 = 12 + 10 – 4
∴ 2y1 + 2y2 + 2y3 = 18
∴ 2(y1 + y2 + y3) = 18
∴ y1 + y2 + y3 = `18/2`
∴ y1 + y2 + y3 = 9 ......(viii)
G(x, y) is the centroid of ΔABC.
∴ By centroid formula,
a = `(x_1 + x_2 + x_3)/3`
∴ x = `3/3` ......[From (iv)]
∴ x = 1
b = `("y"_1 + "y"_2 + "y"_3)/3`
∴ y = `9/3` ......[From (viii)]
∴ y = 3
APPEARS IN
संबंधित प्रश्न
Find the mid-point of the line segment joining the points:
(–6, 7) and (3, 5)
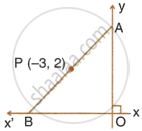
P(–3, 2) is the mid-point of line segment AB as shown in the given figure. Find the co-ordinates of points A and B.
(–5, 2), (3, −6) and (7, 4) are the vertices of a triangle. Find the length of its median through the vertex (3, −6).
The points (2, –1), (–1, 4) and (–2, 2) are mid-points of the sides of a triangle. Find its vertices.
Points A(–5, x), B(y, 7) and C(1, –3) are collinear (i.e. lie on the same straight line) such that AB = BC. Calculate the values of x and y.
A(5, x), B(−4, 3) and C(y, –2) are the vertices of the triangle ABC whose centroid is the origin. Calculate the values of x and y.
Prove that the points A(–5, 4); B(–1, –2) and C(5, 2) are the vertices of an isosceles right-angled triangle. Find the co-ordinates of D so that ABCD is a square.
Find th co-ordinates of the midpoint of the line segment joining P(0, 6) and Q(12, 20).
Find the midpoint of the line segment joining the following pair of point :
(4,7) and (10,15)
ABC is a triangle whose vertices are A(-4, 2), B(O, 2) and C(-2, -4). D. E and Fare the midpoint of the sides BC, CA and AB respectively. Prove that the centroid of the Δ ABC coincides with the centroid of the Δ DEF.
Let A(-a, 0), B(0, a) and C(α , β) be the vertices of the L1 ABC and G be its centroid . Prove that
GA2 + GB2 + GC2 = `1/3` (AB2 + BC2 + CA2)
The midpoint of the line segment joining the points P (2 , m) and Q (n , 4) is R (3 , 5) . Find the values of m and n.
A(3, 1), B(y, 4) and C(1, x) are vertices of a triangle ABC and G(3, 4) is its centroid. Find the values of x and y. Also, find the length of side BC.
Point M is the mid-point of segment AB. If AB = 8.6 cm, then find AM.
The centre ‘O’ of a circle has the coordinates (4, 5) and one point on the circumference is (8, 10). Find the coordinates of the other end of the diameter of the circle through this point.
Point P is midpoint of segment AB where A(– 4, 2) and B(6, 2), then the coordinates of P are ______
Find coordinates of the midpoint of a segment joining point A(–1, 1) and point B(5, –7)
Solution: Suppose A(x1, y1) and B(x2, y2)
x1 = –1, y1 = 1 and x2 = 5, y2 = –7
Using midpoint formula,
∴ Coordinates of midpoint of segment AB
= `((x_1 + x_2)/2, (y_1+ y_2)/2)`
= `(square/2, square/2)`
∴ Coordinates of the midpoint = `(4/2, square/2)`
∴ Coordinates of the midpoint = `(2, square)`
If A(5, 4), B(–3, –2) and C(1, –8) are the vertices of a ∆ABC. Segment AD is median. Find the length of seg AD:
Point M (2, b) is the mid-point of the line segment joining points P (a, 7) and Q (6, 5). Find the values of ‘a’ and ‘b’.
