Advertisements
Advertisements
प्रश्न
Find th co-ordinates of the midpoint of the line segment joining P(0, 6) and Q(12, 20).
उत्तर
P(0, 6) Q(12, 20)
↓ ↓
(x1, y1) (x2, y2)
Let co-ordinates of midpoint be (x, y)
By formula for midpoint.,
=
=
y =
y =
=
= 13
∴ PQ co-ordinates of midpoint of segment PQ are(6, 13)
APPEARS IN
संबंधित प्रश्न
ABCD is a parallelogram where A(x, y), B(5, 8), C(4, 7) and D(2, -4). Find
1) Coordinates of A
2) An equation of diagonal BD
Find the mid-point of the line segment joining the points:
(–6, 7) and (3, 5)
Points A and B have co-ordinates (3, 5) and (x, y) respectively. The mid-point of AB is (2, 3). Find the values of x and y.
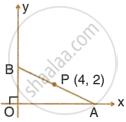
In the given figure, P(4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
Points P(a, −4), Q(−2, b) and R(0, 2) are collinear. If Q lies between P and R, such that PR = 2QR, calculate the values of a and b.
A(5, x), B(−4, 3) and C(y, –2) are the vertices of the triangle ABC whose centroid is the origin. Calculate the values of x and y.
The mid-point of the line segment joining (2a, 4) and (–2, 2b) is (1, 2a + 1). Find the values of a and b.
Find the coordinates of midpoint of the segment joining the points (22, 20) and (0, 16).
A(6, -2), B(3, -2) and C(S, 6) are the three vertices of a parallelogram ABCD. Find the coordinates of the fourth vertex c.
Three consecutive vertices of a parallelogram ABCD are A(S, 5), B(-7, -5) and C(-5, 5). Find the coordinates of the fourth vertex D.
The mid-point of the line segment joining A (- 2 , 0) and B (x , y) is P (6 , 3). Find the coordinates of B.
The three vertices of a parallelogram taken in order are (-1, 0), (3, 1) and (2, 2) respectively. Find the coordinates of the fourth vertex.
Find the mid-point of the line segment joining the points
(8, −2) and (−8, 0)
The mid-point of the sides of a triangle are (2, 4), (−2, 3) and (5, 2). Find the coordinates of the vertices of the triangle
O(0, 0) is the centre of a circle whose one chord is AB, where the points A and B are (8, 6) and (10, 0) respectively. OD is the perpendicular from the centre to the chord AB. Find the coordinates of the mid-point of OD.
A(−3, 2), B(3, 2) and C(−3, −2) are the vertices of the right triangle, right angled at A. Show that the mid-point of the hypotenuse is equidistant from the vertices
If
The ratio in which the x-axis divides the line segment joining the points (6, 4) and (1, −7) is
Find coordinates of midpoint of segment joining (– 2, 6) and (8, 2)
Find coordinates of midpoint of the segment joining points (0, 2) and (12, 14)
