Advertisements
Advertisements
प्रश्न
The mid-point of the sides of a triangle are (2, 4), (−2, 3) and (5, 2). Find the coordinates of the vertices of the triangle
उत्तर
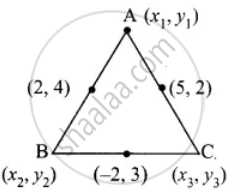
Let the vertices of the ΔABC be A(x1 y1), B(x2, y2) and C(x3, y3)
Mid−point of AB = `((x_1 + x_2)/2, (y_1 + y_2)/2)`
(2, 4) = `((x_1 + x_2)/2, (y_1 + y_2)/2)`
`(x_1 + x_2)/2` = 2
⇒ x1 + x2 = 4 → (1)
`(y_1 + y_2)/2` = 4
⇒ y1 + y2 = 8 → (2)
Mid−point of BC = `((x_2 + x_3)/2, (y_2 + y_3)/2)`
(−2, 3) = `((x_2 + x_3)/2, (y_2 + y_3)/2)`
`(x_2 + x_3)/2` = − 2
⇒ x2 + x3 = − 4 → (3)
`(y_2 + y_3)/2` = 3
⇒ y2 + y3 = 6 → (4)
Mid−point of AC = `((x_1 + x_3)/2, (y_1 + y_3)/2)`
(5, 2) = `((x_1 + x_3)/2, (y_1 + y_3)/2)`
`(x_1 + x_3)/2` = 5
⇒ x1 + x3 = 10 → (5)
`(y_1 + y_3)/2` = 2
⇒ y1 + y3 = 4 → (6)
By adding (1) + (3) + (5) we get
2x1 + 2x2 + 2x3 = 4 – 4 + 10
2(x1 + x2 + x3) = 10
⇒ x1 + x2 + x3 = 5
From (1) x1 + x2 = 4
⇒ 4 + x3 = 5
x3 = 5 – 4 = 1
∴ The vertices of the ΔABC are A(9, 3) B(– 5, 5), C(1, 1)
From (3) x2 + x3 = – 4
⇒ x1 + (– 4) = 5
x1 = 5 + 4 = 9
From (5) ⇒ x1 + x3 = 8
x2 + 10 = 5
x2 = 5 – 10 = – 5
∴ x1 = 9, x2 = – 5, x3 = 1
By adding (2) + (4) + (6) we get
2y1 + 2y2 + 2y3 = 8 + 6 + 4
2(y1 +y2 + y3) = 18
⇒ y1 + y2 + y3 = 9
From (2) ⇒ y1 + y2 = 8
8 + y3 = 9
⇒ y3 = 9 – 8
= 1
From (4)
y2 + y3 = 6
⇒ y1 + 6 = 9
y1 = 9 – 6
= 3
From (6)
y1 + y3 = 4
⇒ y2 + 4
= 9
y2 = 9 – 4
= 5
∴ y1 = 3, y2 = 5, y3 = 1
APPEARS IN
संबंधित प्रश्न
Points P(a, −4), Q(−2, b) and R(0, 2) are collinear. If Q lies between P and R, such that PR = 2QR, calculate the values of a and b.
A(5, x), B(−4, 3) and C(y, –2) are the vertices of the triangle ABC whose centroid is the origin. Calculate the values of x and y.
In the following example find the co-ordinate of point A which divides segment PQ in the ratio a : b.
P(–3, 7), Q(1, –4), a : b = 2 : 1
In the following example find the co-ordinate of point A which divides segment PQ in the ratio a : b.
P(2, 6), Q(–4, 1), a : b = 1 : 2
Find the midpoint of the line segment joining the following pair of point :
( -3, 5) and (9, -9)
A(6, -2), B(3, -2) and C(S, 6) are the three vertices of a parallelogram ABCD. Find the coordinates of the fourth vertex c.
The midpoints of three sides of a triangle are (1, 2), (2, -3) and (3, 4). Find the centroid of the triangle.
Point P is midpoint of segment AB where A(– 4, 2) and B(6, 2), then the coordinates of P are ______
Find coordinates of the midpoint of a segment joining point A(–1, 1) and point B(5, –7)
Solution: Suppose A(x1, y1) and B(x2, y2)
x1 = –1, y1 = 1 and x2 = 5, y2 = –7
Using midpoint formula,
∴ Coordinates of midpoint of segment AB
= `((x_1 + x_2)/2, (y_1+ y_2)/2)`
= `(square/2, square/2)`
∴ Coordinates of the midpoint = `(4/2, square/2)`
∴ Coordinates of the midpoint = `(2, square)`
Point M (2, b) is the mid-point of the line segment joining points P (a, 7) and Q (6, 5). Find the values of ‘a’ and ‘b’.
