Advertisements
Advertisements
प्रश्न
Points P(a, −4), Q(−2, b) and R(0, 2) are collinear. If Q lies between P and R, such that PR = 2QR, calculate the values of a and b.
उत्तर
Given, PR = 2QR
Now, Q lies between P and R, so, PR = PQ + QR
∴ PQ + QR = 2QR
`=>` PQ = QR
`=>` Q is the mid-point of PR.
∴ `(-2, b) = ((a + 0)/2, (-4 + 2)/2)`
`(-2, b) = (a/2, -1)`
`=>` a = −4 and b = –1
APPEARS IN
संबंधित प्रश्न
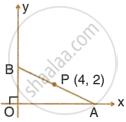
In the given figure, P(4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
P(4, 2) and Q(–1, 5) are the vertices of parallelogram PQRS and (–3, 2) are the co-ordinates of the point of intersection of its diagonals. Find co-ordinates of R and S.
Find the midpoint of the line segment joining the following pair of point :
( -3, 5) and (9, -9)
Find the midpoint of the line segment joining the following pair of point :
( a+3, 5b), (3a-1, 3b +4).
(4, 2) and (-1, 5) are the adjacent vertices ofa parallelogram. (-3, 2) are the coordinates of the points of intersection of its diagonals. Find the coordinates of the other two vertices.
Find the centroid of a triangle whose vertices are (3, -5), (-7, 4) and ( 10, -2).
The mid-point of the line segment joining A (- 2 , 0) and B (x , y) is P (6 , 3). Find the coordinates of B.
The points A(−3, 6), B(0, 7) and C(1, 9) are the mid-points of the sides DE, EF and FD of a triangle DEF. Show that the quadrilateral ABCD is a parallelogram.
The ratio in which the x-axis divides the line segment joining the points A (a1, b1) and B (a2, b2) is
Point M (2, b) is the mid-point of the line segment joining points P (a, 7) and Q (6, 5). Find the values of ‘a’ and ‘b’.
